Humberto e Roberto são dois músicos de jazz gêmeos, que se apresentam como uma dupla tocando trombone e saxofone. Aos vinte anos, no entanto, Roberto recebeu uma irresistível oferta para tocar uma estrela distante anos-luz. Para comemorar sua boa sorte, ele comprou um novo veículo para a viagem – um cupê espacial de luxo que viaja a . Os gêmeos se comprometem a treinar com afinco, de modo a poderem recompor a dupla no futuro. Entretanto, a turnê de Roberto é tão bem-sucedida que ele leva exatos dez anos para voltar e reencontrar Humberto. Após o reencontro:

(a) Quanto anos terá Roberto treinado e

(b) Quanto anos terá Humberto treinado?

(a) A figura abaixo esquematiza a situação no referencial do Roberto. A distância entre a Terra e a estrela é o comprimento da vara em repouso:

Para achar o tempo , no referencial de Roberto, da viagem até a estrela de distância , aplicamos a fórmula:

Contudo, devemos achar , que é relacionado com pela fórmula de contração do espaço:

Substituindo por valores numéricos, a equação achada no Passo 3:

Enquanto Roberto estava na estrela, cada referencial estava em repouso em relação ao outro. Assim, devemos somar ao tempo achado. Como houve uma viagem de ida e uma de volta, o tempo deve ser multiplicado por dois, pois a relatividade ocorreu durante a viagem de Roberto:

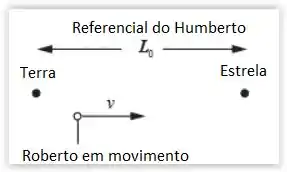
(b) A figura abaixo esquematiza a situação no referencial do Humberto. A distância entre a Terra e a estrela é o comprimento da vara em movimento:

Para achar o tempo no referencial de Humberto para a viagem de Roberto até a estrela, devemos usar a fórmula:

Isolando, obtemos:

Trocando as variáveis pelos valores correspondentes:

Enquanto Roberto estava na estrela, cada referencial estava em repouso em relação ao outro. Assim, devemos somar ao tempo achado. Como houve uma viagem de ida e uma de volta, o tempo deve ser multiplicado por dois, pois a relatividade ocorreu durante a viagem de Roberto: