Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 106

Um bloco de 5,0   k g é lançado para cima em um plano inclinado de 30 ° com uma velocidade de 5,0   m / s . Que distância o bloco percorre (a) se o plano não possui atrito e (b) se o coeficiente de atrito cinético entre o bloco e o plano é   0,40 ? (c) No último caso, qual é o aumento da energia térmica do bloco e do plano durante a subida do bloco? (d) Se o bloco desce de volta submetido à força de atrito, qual é a velocidade do bloco quando chega ao ponto de onde foi lançado?

Passo 1

  1. Oi, galerinha! Tudo bom? Para resolver essa questão vamos usar a lei de conservação:

    2. K 0 + U 0 = K 1 + U 1

    Com isso, a primeira coisa que devemos fazer é definir as condições iniciais do problema. Neste caso vamos usar a base do plano inclinado como referência. Como o bloco é lançado para cima, temos que no momento inicial sua energia pontecial é zero. Já na sua altura máxima, toda sua energia cinérica foi convertida em potencial, logo

    m v 0 2 2 + 0 = 0 + m g y

    Isolando y ,

    y = m v 0 2 2 m g = v 0 2 2 g

    sendo v 0   =   5,0   m / s , temos que

    y = 1,3   m

    A distância d   ao longo do plano está relacionada à altura y pela equação y   =   d   s e n   θ . Como mostrado na figura:

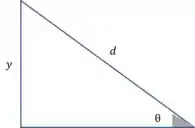
    Com isso,

    1,3 = d   s e n 30

    d = 2,6   m

    Passo 2

  2. Analisando as forças envolvidas , concluímos que o módulo da força de atrito é

    3. f k   =   μ k m g   c o s   θ

    Utilizandos as relações que já conhecemos , obtemos que :

    K 0 + U 0 = K 1 + U 1 + f k d

    m v 0 2 2 + 0 = 0 + m g y + f k d

    m v 0 2 2 = m g d sen ⁡ θ + μ k m g d cos ⁡ θ

    Dividindo ambos os membros pela massa e explicitando d , achamos que :

    d = v 0 2 2 g ( μ k cos ⁡ θ + sen ⁡ θ ) = 1,5   m

    Até aqui de boa? Bora continuar então que ainda não acabou!

    Passo 3

  3. Então galera , nós sabemos que a energia térmica produzida pelo atrito é dada por :

    4. Δ E t   =   f k d   =   μ k   m g d cos ⁡ θ

    Substituindo os valores conhecidos , obtemos que :

      ∆ E t =   26   J

    Passo 4

  4. A descida de volta, da altura y   =   1,5   s e n   30 ° até a base do plano inclinado, também pode ser analisada através da leide conservação de energia . Temos que :

K 1 + U 1 = K 2 + U 2 + ∆ E t

0 + m g y = m v 0 2 2 + 0 + 26 J

o que nos dá v 2 =   2,1   m / s .

Resposta

  1. d = 2,6   m
  2. d = 1,5   m
  3. ∆ E t = 26 J
  4. v 2 = 2,1 m / s

Tranquilo pessoal??? Bora resolver mais questões então!!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja k a constante de uma mola ideal que possui um bloco de massa m preso a uma de suas extremidades. a) O bloco se move de x 1 a x 2 , onde x 2x 1 . Qual o trabalho realizado pela força da mola duran
Um bloco de 0,50k g é empurrado contra uma mola horizontal de massa desprezível, comprimindo a mola até uma distância igual a 0,20m (Figura 7.31). Quando o bloco é libertado, ele se move sobre o topo
Um pedaço de madeira de 2,0k g desliza sobre a superfície mostrada na F i g u r a7.33 . As laterais curvadas da superfície são perfeitamente lisas, mas o fundo horizontal áspero tem 30m de comprimento
O Grande Sandine é um acrobata de circo com massa de 60,0 kg, que é lançado por um canhão (na realidade um canhão com molas). Você não encontra muitos homens com essa bravura, e por isso você o auxili
Subindo e descendo a colina. Uma rocha de 28,0k g se aproxima da base de uma colina com velocidade escalar de 15m / s . Essa colina tem inclinação de baixo para cima a um ângulo constante de 40,0 º º