Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 87

O Homem Aranha salta do topo de um edifício alto. Ele cai em queda livre, a partir do repouso até o solo, por uma distância de h. Ele cai uma distância de h/4 no último 1,0 s da sua queda. Qual é a altura h do prédio?

Passo 1

Oi, galerinha! Tudo bom? Temos aqui um problema sobre queda livre, mas repara que a questão menciona um altura h e um h / 4 , então vamos desenhar para ficar mais claro.

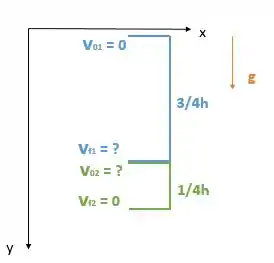
Vamos considerar dois segmentos do movimento: o último 1s e a moção anterior a isso. A velocidade final para o primeiro segmento v f 1   é a velocidade inicial para o segundo segmento ( v 02 ) .

v f 1 =   v 02

Vamos tomar como + y para baixo, então, a y = 9,8 m / s 2

Passo 2

Queremos descobrir a velocidade final da primeira parte, ele nos deu as seguintes informações:

D a d o s :   ∆ y = 3 h 4   a y = 9,8 m / s 2 v 0 y = 0

Como não nos dá e não nos pede o tempo, podemos utilizar a equação de Torricelli:

v f 1 2 = v y 2 = v 0 y 2 + 2 a y ∆ y

v f 1 a velocidade final

v 0 y a velocidade inicial

a y a aceleração

Δ y o deslocamento

Subsituindo os valores que já sabemos:

v f 1 2 =   0 2 + 2.9,8 . 3 h 4

v f 1 = 2.9,8 . 3 h 4

v f 1 = ( 3,834 h )   m / s

Passo 3

Como falamos antes, a velocidade inicial do último trecho de altura igual a h / 4 é igual a velocidade final do primeiro trecho que achamos no passo anterior.

v f 1 =   v 0 2

v 0 2 = ( 3,834 h )   m / s

Para t = 1 s :

∆ y = v 0 2 t + a y t 2 2

Substituindo os valores para esse segundo trecho do caminho:

h 4 = 3,834 h   + 9,8 . 1 2 2

Vamos tomar: h = u 2 . E vamos resolver para u :

1 4 u 2 - 3,834 u - 4,90 m = 0  

Passo 4

Fazendo: a = 1 4 b = - 3,834 c = 4,90 m

podemos utilizar Bhaskara para encontrar u :

u = - b ± b 2 - 4 a c 2 a

u = 2 3,834 ± - 3,834 2 + 4,90

u = 2 ( 3,834 ±   19,6 )

u = 2 ( 3,834 ±   4,427 )

Como só nos interessa o tempo positivo, temos que:

u = 2 ( 3,834 +   4,427 )  

u = 2   .   8,261

u = 16,522

E

h = u 2 = 273 m

Resposta

O edifício tem   273 m de altura.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois grilos, Chirpy e Milada, saltam do topo de um rochedo íngreme. Chirpy simplesmente se deixa cair e chega ao solo em 3.50 s, enquanto Milada salta horizontalmente com velocidadeinicial de 95,0 cm/
Um helicóptero militar em missão de treinamento voa horizontalmente com velocidade de 60,0m / s e acidentalmente deixa cair uma bomba (felizmente não ativa) de uma altura de 300 m . Despreze a resistê
Uma ousada nadadora salta correndo 510 N e horizontalmente de um rochedo para ummergulho, conforme a Figura 3.39. Qual deve ser sua velocidade mínima quando salta do topo do rochedo, de modo que ela c
Uma bola de gude rola horizontalmente com velocidade escalar v 0 e cai do topo de umaplataforma de 2,75m de altura, sem sofrer nenhuma resistência significativa do ar.No nível do solo, a 2,0m da base
Durante uma tempestade, um carro chega onde deveria haver uma ponte, mas o motorista a encontra destruída, levada pelas águas. Como precisa chegar ao outro lado, o motorista decide tentar saltar sobre