Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Problemas - Ex. 46
46. Um indutor de conduz uma corrente que varia com o tempo de acordo com a expressão . Determine uma expressão para a fem induzida em função do tempo. Faça um gráfico para a corrente induzida e para a fem induzida em função do tempo desde até . Qual é a fem máxima? Qual é a corrente quando a fem induzida é máxima? Qual é a corrente máxima? Qual é a fem induzida quando a corrente é máxima?
Passo 1
Primeiro, vamos ver como encontramos a fem tendo a expressão da corrente em função do tempo, temos:
Então basta derivar a função da corrente e multiplicar por que encontramos a fem.
Para achar a fem máxima, basta derivar a expressão que encontrarmos para ela e igualar a zero e achar o valor de que faça isso ser verdadeiro, depois derivamos mais uma vez e vemos se esse valor de faz com que a expressão seja positiva. Essa é a mesma ideia que usamos para achar máximos de funções em cálculo.
Tendo esse valor é só substituir na expressão original e ver o valor para a fem que encontramos.
E para achar a corrente quando essa fem ocorre temos que pegar o mesmo valor de que encontramos para a fem máxima e substituir na expressão da corrente, achando assim acorrente no instante que a fem é máxima.
Para achar a corrente máxima vamos fazer exatamente o mesmo processo que fizemos anteriormente para a fem, só que agora com a expressão da corrente.
E para achar a fem quando essa corrente ocorre temos que pegar o mesmo valor de que encontramos para a corrente máxima e substituir na expressão da fem, achando assim fem no instante que a corrente é máxima.
Passo 2
Vamos encontrar então a expressão para , temos:
Eu passei já que é melhor se trabalhar com .
Lembrando que segundo o enunciado , temos:
Abaixo temos o gráfico dessas duas expressões, para em e em .
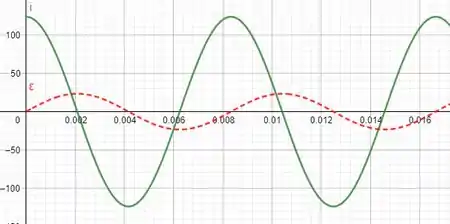
Passo 3
Se você reparar nas expressões que temos para acorrente e a fem, elas são funções periódicas por conta dos termos de cosseno e seno, os valores se repetem com o tempo.
Então temos mais de um valor de que faz com que elas sejam máximas.
Lembrando o que sabemos sobre funções senos e cossenos, lembraremos que os valores máximos dessas funções é , assim temos que:
Que são os termos que multiplicam o cosseno e o seno.
Passo 4
Agora vamos ver que valores de fazem com que o termo cosseno seja igual a , temos:
Se escolhermos , temos:
Que é verdadeiro. Então em temos , substituindo esse valor na fórmula da fem, temos:
Então na corrente máxima temos .
Passo 5
Agora vamos ver que valores de fazem com que o termo cosseno seja igual a , temos:
Então em temos , substituindo esse valor na fórmula da corrente, temos:
Então na fem máxima temos .