Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Exercício - Ex. 05
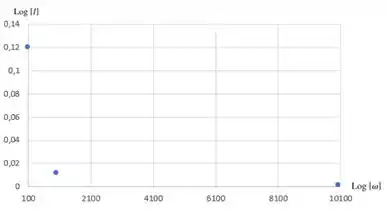
05. Um indutor de com resistência desprezível é conectado através da fonte do Exercício . Calcule a amplitude da corrente para quando a frequência angular for: ; ; . Mostre os resultados de até fazendo um gráfico de contra .
Passo 1
Essa questão nos pede a amplitude da corrente para diferentes frequências angulares que nos foram dadas.
O enunciado nos dá também indutância do indutor , e ele também diz que é a mesma fonte do exercício e através dele sabemos que a amplitude de voltagem é .
Sendo assim usaremos a equação que relaciona tudo o que temos ao que queremos, e esse equação é a equação no nosso livro que diz:
Prontinho, temos o que é necessário para fazer a questão. Agora mãos à obra!
Passo 2
Para .
Substituindo tudo o que temos na equação do Passo 1:
Agora é só repetir em e mudando a .
Passo 3
Para .
Passo 4
Para .
Passo 5
Sendo temos que e são constantes, e e são variáveis, onde depende de .
Sendo assim podemos dizer que:
Resposta
