Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 4.Problemas - Ex. 7

Tudo beleza? Vem comigo em mais esse problema que juntos vamos nos livrar dele.

A equação apresentada acima no enunciado é um dos termos da amplitude de difração em uma dada direção para o caso de fendas. Que é dada por (Eq. ):

Onde é a defasagem entre duas fendas.

Esse fator é uma progressão geométrica que tem como razão , então essa soma pode ser representada por:

Com isso a intensidade do padrão de interferência pode ser escrita da seguinte forma:

E usando o fato de que , temos que:

Só que o termos que vai nos interessar é

Já que é ele que fornece o padrão de interferência. Um exemplo do gráfico dessa expressão é o seguinte:

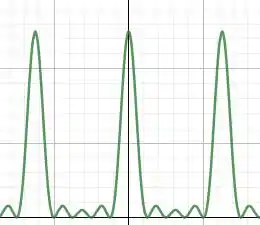
Agora temos que ver que valor de faz com que tenhamos o primeiro mínimo que é o que temos que interpretar no plano complexo.

Vamos lá então, para que a expressão que temos do passo seja zero, precisamos que:

Já que a função seno zero para múltiplos inteiro de .

Isolando , temos:

Onde representa a ordem nos mínimos, como estamos interessados no primeiro temos que , logo temos:

Agora temos que ver o comportamento de com esse valor de para podermos construir o o vetor no plano complexo.

Temos que:

Usando o que temos para ficamos com:

Mas temos que:

Então temos que:

Então a representação dele no plano complexo seria um ponto na origem.

Demonstração acima.