Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 109
Em seu laboratório de física, um bloco de massa está em repouso sobre uma superfície horizontal. Você prende uma corda leve ao bloco e aplica uma força horizontal à extremidade livre da corda. Então, descobre que o bloco permanece em repouso até que a tensão na corda seja superior a . Para , você mede a aceleração do bloco quanto é mantida em um valor constante, e desenha os resultados (Figura P5.109). A equação para a linha reta que melhor se ajusta aos seus dados é .
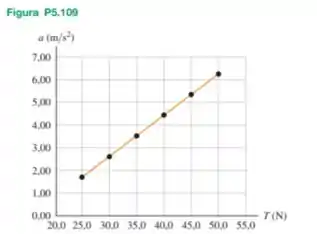
Para esse bloco e superfície: (a) qual é o coeficiente de atrito estático? (b) Qual é coeficiente de atrito cinético? (c) Se o experimento fosse feito na superfície da Lua, onde é muito menor que na Terra, o gráfico de versus ainda se ajustaria bem a uma linha reta?
Passo 1
Fala galerinha, beleza?
Nesse problema vamos brincar um pouco com ajuste de dados e interpretação de um modelo. Nesse tipo de problema, a primeira coisa que deve ser feita é entender bem o modelo!
O enunciado disse que para o bloco fica parada, de modo que essa força limite corresponde a força de atrito estática máxima:
Por outro lado, sabemos que
Como o bloco se encontra num plano horizontal, segue que . Portanto,
Vamos guardar essa informação!
Passo 2
Para o regime passa a ser de atrito cinético. A tração puxa o corpo para frente e o atrito atua como uma resistência para trás:
Como , segue que
Logo,
Por outro lado, o enunciado disse que
Com isso podemos achar e :
Desta forma, já respondemos o item (b):
Para responder o item (a), voltamos ao resultado do passo 1:
Passo 3
No item (c), temos que analisar o que aconteceria se fossemos para a Lua. Observe que a relação
continuaria válida! Logo, o gráfico seguiria sendo uma reta! Observe que o coeficiente angular não seria alterado, de modo que a reta teria a mesma inclinação. O que ia mudar é o coeficiente linear, pois na Lua tem outro valor.