Em seu laboratório de física, um oscilador é preso à extremidade de uma corda horizontal. A outra extremidade da corda passa por uma polia sem atrito. Você suspende uma massa M pela extremidade livre da corda, produzindo a tensão Mg na corda. O oscilador produz ondas transversais de frequência f sobre a corda. Você não varia essa frequência durante o experimento, mas testa as cordas com três densidades lineares µ diferentes. Você também mantém uma distância fixa entre a extremidade da corda onde o oscilador está preso e o ponto onde ela está em contato com a borda da polia. Para produzir ondas estacionárias na corda, você varia M; então, você mede a distância d de um nó para outro para cada padrão de onda estacionária e obtém os seguintes dados:
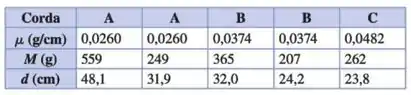
(a) Explique por que você obtém apenas certos valores de d. (b) Represente graficamente µd2 (em kgm) em função de M (em kg). Explique por que os dados desenhados dessa forma devem ficar próximos a uma linha reta. (c) Use a inclinação do melhor ajuste dos dados à linha reta para determinar a frequência f das ondas produzidas na corda pelo oscilador. Considere g = 9,80 m/s2. (d) Para a corda A (µ,= 0,0260 g/cm), que valor de M ( em gramas) seria necessário para produzir uma onda estacionária com uma distância de 24,0 cm de um nó a outro? Use o valor de f calculado no item (c).
Passo 1
Fala galera, bora lá!
(a) Para a resolução desta questão será utilizado o aspecto relativo à distância entre dois nós consecutivos de uma onda estacionária, no qual prediz que tal distância é equivalente a meio comprimento de onda:
: distância entre dois nós concecutivos
: comprimento de onda
Passo 2
A distância foi medida para cada situação de contorno do experimento, ou seja, para determinados valores de densidades lineares () da corda e de massa () fixada na mesma.
Sabe-se que o comprimento de uma onda estacionária () relaciona-se com a velocidade da onda e a frequência de propagação a partir da seguinte formulação:
: velocidade
: comprimento de onda
: frequência
Passo 3
Sabe-se também que a velocidade de propagação de uma onda estacionária em uma corda é determinada pela seguinte expressão:
: velocidade
: tensão
: densidade linear
Por sua vez, a tensão produzida na corda pela massa () equivale ao peso do objeto fixado na mesma:
: massa
: aceleração da gravidade (
Passo 4
Assim, substituindo-se os termos relativos a tensão (), a velocidade de propagação () e ao comprimento de onda () na equação que fornece a distância () entre os dois nós consecutivos, obtêm-se a seguinte formulação:
Logo, apesar da frequência se manter constante durante o experimento, percebe-se que a distância () entre os dois nós é diretamente proporcional a massa () do objeto fixado na corda e inversamente proporcional a densidade linear () da corda.
Passo 5
Portanto, certos valores de foram assim obtidos devido à influência da massa () do objeto e da densidade linear () da corda, características estas que foram alteradas no experimento.
Passo 6
(b) Para a resolução desta questão será plotada curva referente aos pontos formados pelos dados do experimento e utilizado o conceito de função linear para caracteriza-la.
Abaixo segue a imagem com a plotagem do gráfico dos dados, bem como a tabela com os valores utilizados:
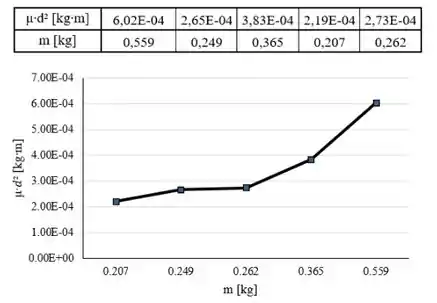
Passo 7
A curva deve se aproximar de uma reta devido à natureza da equação gerada a partir do produto entre a densidade linear () da corda e o quadrado da distância que corresponde a:
Considerando que refere-se à variável pertencente aos eixos das abcissas do gráfico, a equação resultante representa uma função linear de 1º grau, caracterizando uma reta.
Portanto, a curva da função resultante plotada no gráfico aproxima-se de uma reta devido à natureza de sua equação que corresponde a uma função linear de 1º grau.
Passo 8
(c) Para a resolução desta questão será utilizado o preceito de que a derivada de uma função qualquer corresponde numericamente à tangente do ângulo de inclinação da reta tangente à curva desta função.
Como a função avaliada refere-se a uma reta, a reta tangente à curva desta função coincide com a mesma.
Passo 9
Sabe-se que a tangente do ângulo de inclinação de uma reta qualquer pode ser determinada conhecendo-se dois pontos pertencentes a tal reta a partir da expressão abaixo:
Passo 10
Para um melhor ajuste dos valores, considerou-se uma reta interligando o primeiro ponto da curva ao último ponto da curva . Logo, a tangente do ângulo de inclinação da reta corresponde a:
A derivada da função correspondente a reta - cuja equação foi previamente determinada no item (b) - corresponde a:
Passo 11
Como a derivada da função é numericamente igual à tangente do ângulo de inclinação, pode-se determinar o valor da frequência a partir das seguintes operações abaixo:
Portanto, a frequência das ondas produzidas na corda corresponde a:
Passo 12
(d) Para a resolução desta questão será utilizada a equação para a determinação do valor da distância referente aos nós das ondas produzidas, equação esta previamente determinada no passo 4 e correspondente a:
Conhecendo-se os valores relativos a frequência, densidade linear e distância entre nós, pode- se determinar o valor da massa:
Portanto, o valor correspondente à massa necessário para que a distância entre os nós das ondas produzidas seja equivalente a 24 cm corresponde a:
Resposta
- Portanto, certos valores de foram assim obtidos devido à influência da massa () do objeto e da densidade linear () da corda, características estas que foram alteradas no experimento.
- Resolvido no passo 6.