Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 128
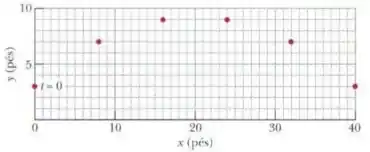
O lançador em uma partida de softball arremessa a bola de um ponto situado pés acima do solo. Um gráfico estroboscópico da posição da bola é mostrado na figura, onde as leituras estão separadas por e a bola foi lançada em . (a) Qual é o módulo da velocidade inicial da bola? (b) Qual é o módulo da velocidade da bola no instante em que atinge a altura máxima em relação ao solo? (c) Qual é essa altura máxima?
Passo 1
(a) Nosso primeiro objetivo é encontrar o módulo da velocidade inicial da bola. Uma forma de fazer isso é encontrar cada uma das componentes iniciais e e então fazer:
Essas velocidades aparecem nas fórmulas para as coordenadas e da bola:
E temos que nos lembrar de usar a aceleração da gravidade em unidades do sistema imperial, já que o gráfico também está nessas unidades:
Passo 2
(a) Para encontrar os valores de e vamos usar o sexto ponto do gráfico, que tem coordenadas ) e corresponde ao instante .
Começando por :
E agora . Perceba que nesse quinto ponto :
E agora podemos calcular o módulo da velocidade:
Passo 3
(b) No instante em que a bola atinge a altura máxima a sua velocidade vertical é nula, e ela tem apenas a componente horizontal da velocidade.
Mas essa componente é constante! Ou seja, ela não muda desde o início do movimento. Então podemos pegar o resultado que já encontramos para a velocidade horizontal inicial :
Passo 4
(c) Para encontrar a altura máxima, vamos pensar no seguinte: a bola leva para chegar na mesma altura em que foi lançada, certo?
Como a bola atinge a altura máxima exatamente na metade do movimento, o instante de tempo em que isso acontece é:
E podemos usar a equação lá de cima para encontrar a coordenada nesse instante:
Pelo gráfico podemos ver que :
Resposta
(a) .
(b) .
(c) A altura máxima é .