Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 7.Problemas - Ex. 6
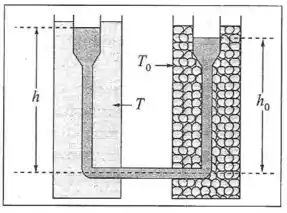
(a) Um líquido tem coeficiente de dilatação volumétrica . Calcule a razão entre a densidade do líquido à temperatura e sua densidade à temperatura . (b) No método de Dulong e Petir para determinar , o líquido é colocado num tubo em U, com um dos ramos imerso em gelo fundente (temperatura ) e o outro em óleo aquecido à temperatura . O nível atingido pelo líquido nos dois ramos é, respectivamente medido pelas alturas e . Mostre que a experiência permite determinar (em lugar do coeficiente de dilatação aparente do líquido), e que o resultado independe de o tubo em U ter secção uniforme. (c) Numa experiência com acetona utilizado este método, é , é , e . Calcule o coeficiente de dilatação volumétrica da acetona.
Passo 1
A densidade do líquido à temperatura :
Onde é o volume à temperatura . Quando a temperatura aumenta, o volume do líquido é dado por:
E então sua nova densidade é:
E a razão entre as densidades é:
E podemos usar uma aproximação para simplificar melhor esse resultado:
Então:
Passo 2
(b) Vamos começar igualando as pressões nos fundos de cada um dos ramos do tubo:
Perceba que o líquido nos dois ramos é o mesmo, “óleo” e “gelo” são os materiais em torno de cada tubo:
E agora podemos aproveitar a fórmula que encontramos no passo anterior:
Obs.: estamos usando a fórmula sem a aproximação que fizemos.
E assim chegamos em uma fórmula para determinar o coeficiente de dilatação :
Aqui já é visível que o resultado não depende do tubo ter seção uniforme.
Passo 3
(c) Agora vamos usar a nossa fórmula para calcular o da acetona:
Substituindo os valores numéricos que foram dados no enunciado:
Resposta
(a) A razão é .
(b) O coeficiente de dilatação volumétrica é .
(c) .