Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.4 - Ex. 39

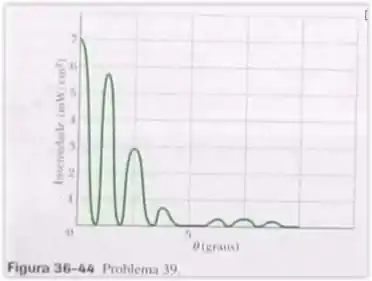
Uma luz com um comprimento de onda de 440   n m passa por um sistema de dupla fenda e produz uma figura de difração cujo gráfico de intensidade I em funções da posição angular θ aparece na Fig. 36-44. Determine (a) a largura das fendas e (b) a distância entre as fendas. (c) Mostre que as intensidades máximas indicadas para as franjas de interferência com m = 1 e m = 2 então corretas.

Passo 1

A difração por uma rede de N ranhuras produz máximos em ângulos θ tais que

d   s e n   θ = m d λ

Os máximos de difração e d a distância entre as fendas

e para interferência teremos

a   s e n   θ = m a λ

os mínimos, a a largura da fenda

A intensidade I para um ângulo θ é dada por

I θ = I m ( cos 2 ⁡ β )   s e n   α α 2

Onde

β = π d λ s e n   θ e α = π a λ s e n   θ

Passo 2

  1. Pela figura temos que o primeiro mínimo de difração é observado em θ = 5 °

    2. Então

    a = λ s e n   θ = 440   n m s e n   5 ° = 5   μ m

    Passo 3

  2. Pela figura temos também que a quarta franja lateral está ausente, isso implica que o máximo da difração coincide com o primeiro mínimo da figura de interferência. Desta forma temos que

    3. d a = 4 → d = 4 a = 20   μ m

    Passo 4

  3. Para a franja de interferência em m = 1 , temos θ = 5 / 4

α = π a   s e n   θ λ = π 5   μ m s e n   1,25 ° 440   n m = 0,787   r a d

Assim

I = I m s e n   α α 2 = 7,0 m W c m 2 s e n 0 , 787   r a d 0,787   r a d 2 = 5,7   m W / c m 2

Que aparentemente bate perfeitamente.

Para a franja de interferência em m = 2 , temos θ = 5 / 2

α = π a   s e n   θ λ = π 5   μ m s e n   2 , 5 0 ° 440   n m = 1 , 57   r a d

Assim

I = I m s e n   α α 2 = 7,0 m W c m 2 s e n 1,57   r a d 1,57   r a d 2 = 5,7   m W / c m 2

Que aparentemente bate perfeitamente também.

Resposta

  1. 5   μ m
  2. 20   μ m
  3. m = 1 → I = 5,7 m W c m 2 ; m = 2 → I = 2,8   m W / c m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No experimento de dupla fenda da Fig. 35-10, o ângulo θ é 20 ° , a distância entre as fendas é 4,24 μ m e o comprimento de onda é λ = 500 n m . (a) Que múltiplo de λ corresponde à diferença de fase em
Em um experimento de dupla fenda, a distância entre as fendas é 5 m m e as fendas estão a 1 m de distância da tela. Duas figuras de interferência são vistas na tela, uma produzida por uma luz com um c
Na fig 35-37, as fontes AeB , emitem ondas de rádio de longo alcance com um comprimento de onda de 400 m , com a fase da onda emitida pela fonte A adiantada de 90 ° , em relação à onda emitida pela fo
Na fig 35-36, duas fontes pontuais isotrópicas, S 1 eS 2 , emitem ondas luminosas em fase cujo comprimento de onda é λ . As fontes estão sobre o eixo x , separadas por uma distância d , e um detector
Na fig 35-39 duas fontes pontuais isotrópicas, S 1 eS 2 , estão no eixo y , separadas por uma distância de 2,7 μ m , e emitem em fase com um comprimento de onda de 900 n m . Um detector de luz é coloc