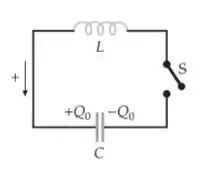
Um indutor e um capacitor estão conectados como mostra a figura 29-30. Inicialmente a chave está aberta e a placa esquerda do capacitor tem uma carga . A chave é, então, fechada. (a) Faça um gráfico de e no mesmo gráfico e explique como pode ser visto nestas duas curvas que a corrente está adiantada em relação à carga por . (b) As expressões para a carga e para a corrente são dadas pelas Equações 29-38 e 29-39, respectivamente. Use trigonometria e álgebra para mostrar que a corrente está adiantada em relação à carga por .

Faaaaaaaaala meu dignissimo, tudo certinho?

Vamos começar a entender esse problema, que rapadura é doce mas não é mole não!

O problema fala de um que aqui representa a carga instantânea no capacitor, e aqui podemos usar aquela regrinha do Loop de Kirchhoff para obtermos a equação diferencial para o circuito (lembra que EDO é uma equação onde a incógnita é uma função).

Depois de encontrada, poderemos EDO para obter uma expressão para a carga no capacitor em função do tempo e, derivando em relação ao tempo, chegaremos a uma expressão para o corrente em função do tempo. Usaremos um programa para traçar os gráficos.

Aplique a regra de loop de Kirchhoff a um loop no sentido horário logo após a chave ser fechada:

Porque :

Ou até mesmo:

A solução para esta equação é:

Onde:

Porque e:

A corrente no circuito é a derivada de em relação a :