Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 107
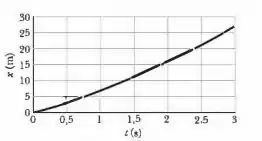
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante . O gráfico de em função de aparece na Fig. 2-44, onde é tomado como o instante em que o vento começou a soprar e o sentido positivo do eixo é para leste. (a) Qual é a aceleração do trenó durante o intervalo de ? (b) Qual é a velocidade do trenó no final do intervalo de ? (c) Se a aceleração permanece constante por mais , qual é a distância percorrida pelo trenó no segundo intervalo de ?
Passo 1
O enunciado já diz que a aceleração é constante, então este é um problema de MRUV. Para resolver este exercício, como não foi dado nenhum valor além do gráfico, vamos ter que buscar os dados extraindo valores do gráfico.
Como este é um gráfico da posição em função do tempo, vamos usar a função da posição:
Alpem disso também vamos precisar de dois pontos quaisquer para encontrar a aceleração e a velocidade , pois conseguimos definir que olhando diretamente o gráfico. Depois, usaremos a função da velocidade:
Para calcular a velocidade no final dos .
Partiu...
Passo 2
Substituindo os pontos e na função da posição para encontrar a aceleração , temos:
Isolando nas duas equações:
Igualando as duas equações:
Logo:
Passo 3
Com o valor da aceleração em mãos substituimos em uma das funções de posição usando os pontos já extraídos do gráfico anteriormente para encontrar a velocidade inicial :
Isolando o :
Com esta velocidade em mãos, podemos usar a função da velocidade para determinar a velocidade no final dos :
Passo 4
Para calcular a distância percorrida pelo trenó no segundo intervalo de vamos iniciar calculando a velocidade nesse instante:
E então, aplicaremos a equação de Torricelli nos instantes e :
Isolando o :
Resposta
- ;
- ;
- .