Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo R.1 - Ex. 30

Maria é uma funcionária de uma grande plataforma espacial. Ela coloca o relógio A no ponto A e o relógio B no ponto B , distante 100 minutos-luz do ponto A . Ela também coloca uma lâmpada de flash em um ponto a meio caminho entre os pontos A e B . José, funcionário de outra plataforma, está junto ao relógio C . Cada relógio é disparado ao ser atingido por um flash. A plataforma de Maria viaja com uma rapidez de 0,600 c para a esquerda, em relação a José. Quando a plataforma de Maria passa pela de José, o relógio B , depois a lâmpada de flash e depois o relógio A passam diretamente em frente ao relógio C . Quando a lâmpada passa perto do relógio C , ela emite um flash e o relógio C começa a marcar a partir do zero.

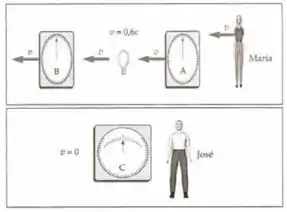
30. De acordo com José:

(a) Qual a distância entre a lâmpada e o relógio em A ?

(b) Qual a distância percorrida pela luz do flash até alcançar o relógio A ?

(c) Qual a distância percorrida pelo relógio A enquanto a luz do flash viaja da lâmpada até ele?

Passo 1

(a) A distância em repouso L 0 entre a lâmpada e o relógio A é 50,0   minutos-luz e está relacionada à distância L medida por José de acordo com a fórmula da contração do comprimento, a seguir:

L = L 0 1 - v 2 c 2

Vamos, então, substituir os valores numéricos pertinentes a cada variável:

L = ( 50   m i n - l u z ) 1 - ( 0,600 c ) 2 c 2

L = 40   m i n u t o s - l u z

Passo 2

(b) José vê o flash viajando para longe dele com uma velocidade de 1,0 c e o relógio A aproximando-se a 0,60 c . Logo, a velocidade relativa da luz do flash é a soma dessas duas velocidades, portanto igual a 1,60 c .

Para, encontrar a distância percorrida pela luz do flash até alcançar o relógio A , precisamos do intervalo de tempo, ∆ t . Basta, então, uma simples razão de espaço percorrido sobre a velocidade:

∆ t = ∆ s v

O espaço percorrido é a distância L , igual a 40   minutos-luz, da letra (a); e a velocidade é igual a 1,60 c .

∆ t = 40   c ∙ m i n 1,6 c

∆ t = 25,0   m i n

O intervalo de tempo percorrido pela luz do flash foi de 25 minutos. Ora bolas! Se a luz do flash viaja na velocidade da luz c , então a distância percorrida foi de 25 minutos-luz.

Passo 3

(c) Vamos expressar a distância percorrida d pelo relógio A enquanto o flash está viajando até ele, em termos da velocidade do relógio A e o tempo ∆ t que leva para o flash o alcançar:

d = v ∆ t

Temos que a velocidade do relógio A é de 0,60 c e o tempo percorrido, foi o encontrado na letra (b), igual a 25 minutos. Vamos substituir esses valores, para achar nossa distância:

d = ( 0,600 c ) ( 25   m i n )

d = 25   m i n u t o s - l u z

Resposta

a) 40 minutos-luz

b) 25 minutos

c) 25 minutos-luz

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5. Dois eventos são simultâneos em um referencial, no qual eles também ocorrem na mesma localização. Eles serão simultâneos em todos os outros referenciais?
6. Dois observadores inerciais estão em movimento relativo. Sob quais circunstância eles podem concordar sobre a simultaneidade de dois eventos diferentes?
8. Verdadeiro ou Falso:(a) A rapidez da luz é a mesma em todos os referenciais(b) O intervalo próprio de tempo é o menor intervalo de tempo entre dois eventos(c) O movimento absoluto pode ser determin
7. A energia total aproximada de uma partícula de massa m que se desloca com uma rapidez v ≪ c é:(a) m c 2 + 1 2 m v ² ²(b) m v ² ²(c) c m v (d) 1 2 m c ² ²
9. Responda os seguintes itens:(a) Mostre que p c tem dimensões de energia.