Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.Problemas Adicionais - Ex. 99
Determine a amplitude angular das oscilações de um pêndulo simples para a qual a diferença entre o torque restaurador necessário para o movimento harmônico simples e o torque restaurador verdadeiro é igual a . (Veja “Expansões Trigonométricas” no apêndice E.)
Passo 1
Tá, essa questão é bastante específica, e até recomenda que você leia o apêndice mencionado ali. Mas não se preocupe, dá pra resumir um pouco aqui.
Sabe aquela equação que você costuma usar pro movimento harmônico simples?
Então, ela é a solução daquela EDO do oscilador harmônico.
Quando a gente monta essa EDO pro caso do pêndulo, acabamos sendo obrigados a fazer uma aproximação pro torque que puxa o pêndulo de volta pro ponto de equilíbrio.
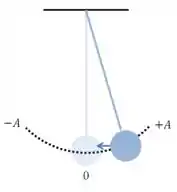
Sem entrar em muitos detalhes, a aproximação é essa aqui:
Onde é comprimento do pêndulo. Ou seja, ela pressupõe o seguinte:
Onde é o ângulo de desvio da corda em relação ao equilíbrio. Essa aproximação é muito boa quando o ângulo não passa de um valor muito alto.
Passo 2
A questão quer saber qual é o ângulo de desvio máximo, quando o “erro” dessa aproximação aí é igual a , então vamos achar uma fórmula pra calcular esse erro.
Usando a fórmula padrão pro erro relativo:
Achamos o seguinte:
Vamos cortar todos os :
Passo 3
Resolver essa equação aí é um problemaço. Você pode ou tentar usar algum método numérico, usar uma expansão de Taylor ou simplesmente chutar alguns valores na calculadora até achar uma resposta próxima.
Obs.: Não se preocupe, essa é uma questão de “aprofundamento”, não deve aparecer em provas justamente por ter uma equação que não tem solução analítica.
Resolvendo no computador, achamos o seguinte:
Ou seja, esse é ângulo de desvio que gera um erro de . Se o ângulo de desvio do pêndulo passar disso, vai estourar o limite de erro que a questão estipulou.
Portanto:
Resposta