Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 41

Um capacitor de placas paralelas preenchido com ar tem uma capacitância de   0,14   μ F . As placas estão separadas por 0,50   m m .

(a) Qual é a área de cada placa?

(b) Qual é a diferença de potencial entre as placas se a placa carregada positivamente tem uma carga de 3 , 2   µ C ?

(c) Qual é a energia armazenada?

(d) Qual é a energia máxima que este capacitor pode armazenar antes que ocorra a ruptura dielétrica entre as placas?

Passo 1

Cara... Imagina um capacitor de placas paralelas de área desconhecida (por enquanto)...

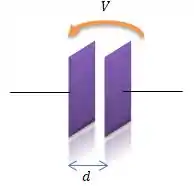
Bem, sabendo que d = 0,50   m m e que esse capacitor tem uma capacitância de C =   0,14   μ F , podemos descobrir tudo que quisermos nesse problema! Preparado?

Passo 2

L e t r a   A :

POW! Podemos determinar a área desse capacitor sabendo que a área está intimamente ligada à capacitância C ...

C = ε 0 A d

Então...

A = C d ε 0

Como d = 0,50   m m = 0,5 ⋅ 10 - 3 m , C =   0,14   μ F = 0,14 ⋅ 10 - 6   F e ε 0 = 8,85 ⋅ 10 - 12   C 2 / N m 2 ...

A = 0,14 ⋅ 10 - 6 ⋅ 0,5 ⋅ 10 - 3 8,85 ⋅ 10 - 12   →

A = 0,14 ⋅ 0,5 8,85 ⋅ 10 3   →

A = 0,0079 ⋅ 10 3   →

A = 7 , 9   m 2

Passo 3

L e t r a   B :

Podemos determinar a diferença de potencial em um capacitor pela relação...

Q = C V   →

V = Q C     →

Como conhecemos a carga Q = 3 , 2   µ C = 3,2 ⋅ 10 - 6   C e a capacitância C = 0,14 ⋅ 10 - 6   F ...

V = 3,2 ⋅ 10 - 6 0,14 ⋅ 10 - 6     →

V = 22,86   V

Passo 4

L e t r a   C :

Já para a energia armazenada...

U = 1 2 C V 2

Então...

U = 1 2 0,14 ⋅ 10 - 6 22,86 2   →  

U = 0,07 ⋅ 10 - 6 522,58   →  

U = 36,58 ⋅ 10 - 6 →

Ou ainda...

U = 36,58   μ J

Passo 5

L e t r a   D :

A ruptura dielétrica no capacitor acontece quando o campo elétrico atinge o valor de ruptura...

E = 30 k V c m

A tensão para esse campo elétrico vai ser...

V = E d   →

V = 30 k V c m ⋅ 0,50   m m

Para transformar de m m para c m , basta andar com a vírgula uma casa para a esquerda...

V = 30 k V c m ⋅ 0 , 0 50   c m   →

V = 1,5   k V

A energia armazenada então vai ser...

U = 1 2 C V 2   →

U = 1 2 0,14 ⋅ 10 - 6 1,5 ⋅ 10 3 2   →

U = 1 2 0,14 ⋅ 10 - 6 1,5 2 ⋅ 10 6   →

U = 1 2 0,14 1,5 2   →

U = 0,1575   J

Ou ainda...

U = 157,75   m J

Resposta

Letra A:

A = 7,9   m 2

Letra B:

V = 22,86   V

Letra C:

U = 36,58   μ J

Letra D:

U = 157,75   m J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a Terra como uma esfera condutora. (a) Qual é sua autocapacitância? (b) Considere que a magnitude do campo elétrico na superfície da Terra seja de 150V / m . A que densidade de carga isto co
Na preparação para um experimento que você fará em seu laboratório de introdução à física nuclear, você está olhando o lado interno de um tubo Geiger. Você mede o raio e o comprimento do fio central d
Um capacitor cilíndrico consiste em um longo fio que tem um raio R 1 , comprimento L e carga + Q . O fio está encoberto por uma casca cilíndrica coaxial externa que tem raio interno R 2 , comprimento
Uma esfera condutora isolada de raio R tem carga Q distribuída uniformemente sobre sua superfície. Determine a distância R ' do centro da esfera tal que metade da energia eletrostática total do sistem
Um capacitor esférico é composto de uma esfera interna que tem raio R 1 e carga + Q , e uma fina casca esférica concêntrica que tem raio R 2 , e carga - Q . (a) Determine o campo elétrico e a densidad