Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 12d

Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidade de carga (fig.).

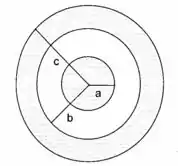
Calcule o campo elétrico na região c ≤ r .

Passo 1

Se liga! Para calcular o campo elétrico, aqui a maneira mais simples de fazer é aplicando a lei de Gauss

ϕ = E A = q i n t ϵ 0

Estamos interessados na região c ≤ r .

Passo 2

Mas olha a figura.

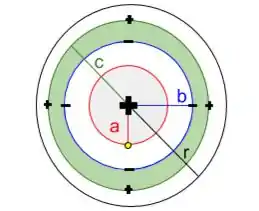
Repare que a carga localizada no centro no interior da superfície gaussiana de raio r é a soma das cargas da esfera e da casca.

Então, vamos calcular as cargas?

Passo 3

Sabemos que a densidade volumétrica de carga é

ρ = q e s f e r a V   ⟹ q e s f e r a = ρ 4 3   π a 3

A carga da casca faremos do mesmo jeito, só precisamos ter a sacada que o volume da casca é

Δ V = 4 3 π ( c 3 - b 3 )

Logo,

q c a s c a =   ρ 4 3 π ( c 3 - b 3 )

E

q i n t = 4 3 ρ π ( a 3 + c 3 - b 3 )

Passo 4

A área será a áreda da esfera de raio r

A = 4 π r 2

Substituindo as expressões de q i n t e A na expressão do fluxo temos

E =   4 3 ρ π ( a 3 + c 3 - b 3 ) 4 π ϵ 0 r 2 = ρ ( a 3 + c 3 - b 3 ) 3 ϵ 0 r 2

Como o campo aponta para fora na direção radial, temos

E → =   ρ ( a 3 + c 3 - b 3 ) 3 ϵ 0 r 2 r ^

Resposta

E → =   ρ ( a 3 + c 3 - b 3 ) 3 ϵ 0 r 2 r ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera sólida não condutora tem diâmetro igual a 1,20m , tem seu centro no eixo x em x = 4,00m e tem uma densidade volumétrica uniforme de carga de + 5,00μ C / m 3 . Uma fina casca esférica não co
Considere um modelo simples, mas surpreendente preciso para a molécula de hidrogênio: duas cargas puntiformes positivas, cada uma com carga + e , estão localizadas no interior de uma esfera uniformeme
Uma pequena superfície gaussiana na forma de um cubo tem faces paralelas aos planos x y , x z e y z (Figura 22-47) e está em uma região na qual o campo elétrico é paralelo ao eixo x . (a) Usando a apr
11 . Uma carga puntiforme igual a 6,20μ C está no centro de um cubo cuja aresta possui um comprimento de 0,500m . ( a ) Qual é o fluxo elétrico através de cada uma das seis faces docubo? ( b ) O que m
7 . Conforme discutimos na Seção 22.5 , as células nervosas humanas possuem carga líquida negativa e o material no interior da célula é um bom condutor. Se uma célula possui carga líquida igual a - 8,