Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 47

Uma mola com constante elástica k está suspensa verticalmente por um suporte, e uma massa m é presa à outra extremidade. A massa inicialmente é mantida parada na posição em que a mola não está esticada. Então, a massa é liberada e passa a oscilar. O ponto mais baixo atingido nas oscilações encontra-se 20 cm abaixo do ponto de onde a massa foi liberada. Qual é a frequência de oscilação?

Passo 1

Veja a figura abaixo que representa o que o enunciado está tentando nos dizer:

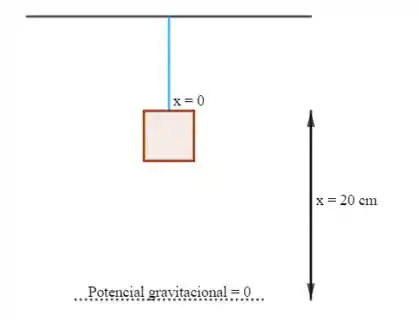
Inicialmente, a caixinha está presa a uma mola (a mola foi representada pela linha azul!) na posição em que a mola está relaxada (não está nem comprimida nem esticada).

Nessa posição a caixinha possui uma energia E :

E i = U + K E i = m g h + 0 E i = m g h

onde K = 0 (já que ela estava inicialmente em repouso) e h é a altura da caixa em relação ao ponto onde o potencial gravitacional é nulo!

No final, a caixa está novamente em repouso. Logo,

E f = U + K E f = 1 2 k h 2 + 0 E f = 1 2 k h 2

A conservação da energia nos garante que

E i = E f

Passo 2

Como

E i = E f m g h = 1 2 k h 2 k m = 2 g h k m = 2 9,8 0,2 k m = 98 1 s 2

Passo 3

Lembrando que:

ω = k m ω = 98 ω = 9,90   r a d / s

Passo 4

Finalmente, temos que

ω = 2 π f f = ω 2 π f = 1,58   H z

Resposta

A frequência é de 1,58   H z .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função velocidade v t aparece na figura se a função posição x ( t ) é da forma x = x m c o s ⁡ ( ω t + φ ) ? A escala do eixo vertical é definida
Qual é a constante de fase do oscilador harmônico cuja função posição x ( t ) aparece na figura se a função posição é da forma x = x m c o s ⁡ ( ω t + φ ) ? A escala do eixo vertical é definida por x
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A Fig. 15-51 mostra a posição x t de um bloco que oscila em um MHS na extremidade de uma mola t s = 40,0 m s . Qual é (a) a velocidade e (b) o módulo da aceleração radial de uma partícula no movimento
Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?