Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 12

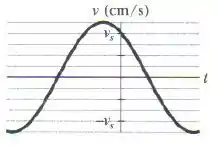
Qual é a constante de fase do oscilador harmônico cuja função velocidade aparece na figura se a função posição é da forma ? A escala do eixo vertical é definida por .

Passo 1

Vamos lá, a função posição do oscilador é essa aqui:

Mas a função representada no gráfico é a da velocidade. Podemos achar ela derivando a função posição em relação ao tempo:

Agora sim, temos a função que descreve a curva no gráfico.

Passo 2

Queremos saber qual é a constante de fase, ou seja, aquele que fica dentro da função trigonométrica.

Pra começar, vamos achar o ponto em que o gráfico cruza o eixo , as coordenadas são:

E substituir isso na função da velocidade:

Ou seja:

Agora falta achar o valor de .

Passo 3

Vamos usar outra informação que o gráfico dá. Olhando bem pra função da velocidade:

Como a função seno varia entre e , o valor máximo que essa função assume é:

Dá pra ver isso no gráfico? Sim! O valor máximo que a curva atinge é justamente o . A gente chega nessa conclusão vendo que cada linha horizontal ali “vale” , e o pico da curva está na quinta linha acima do zero. Então:

Agora substituindo isso ali em cima:

E então:

Que tem infinitas soluções, mas se nos limitarmos a valores entre e

Ou:

Resposta

(a)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função posição x ( t ) aparece na figura se a função posição é da forma x = x m c o s ⁡ ( ω t + φ ) ? A escala do eixo vertical é definida por x

A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v

A Fig. 15-51 mostra a posição x t de um bloco que oscila em um MHS na extremidade de uma mola t s = 40,0 m s . Qual é (a) a velocidade e (b) o módulo da aceleração radial de uma partícula no movimento

Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?

17. Sobre um trilho de ar sem atrito, horizontal, um corpo oscila na extremidade de uma mola ideal de constante 2,50N / c m . O gráfico da Figura 13.31 mostra a aceleração do corpo em função do tempo.