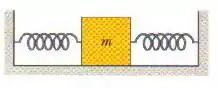
Na figura, duas molas iguais, de constante elástica , estão ligadas a um bloco de massa . Qual é a frequência de oscilação no piso sem atrito?
Passo 1
Show de bolinhas pessoal, essa questão exige um conhecimento maior da equação diferencial que expressa a função do oscilador harmônico. Mas vamos com calma galerinha...

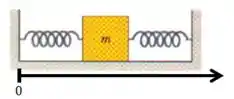
Pensando só nas forças agora. Vamos escolher um sentido pra chamar de positivo e um ponto pra chamar de zero, desse jeito, saca só:
Passo 2
Belezera, agora vamos usar a fórmula da força elástica pra escrever a equação da força de cada mola.
Começando pela mola da esquerda: quando o bloco vai pra frente no sentido positivo, a mola tende a puxar ele de volta pra trás, ou seja:
O sinal de negativo indica que a força é contrário ao movimento do bloco, atuando no sentido de restaurar a posição inicial do bloco.
Agora a mola da direita: Quando o bloco vai pra frente, a mola é comprimida de forma que a força que ela exerce sobre o bloco empurra ele pra trás, como novamente temos que a força é contrário ao sentido do movimento, temos que:
Faz sentido, né? As duas molas querem manter o bloco onde ele está, então é compreensível que as forças tenham fórmulas iguais.
Sendo assim, a força resultante é dada como:
E como estamos falando de um força resultante, então quer dizer que também possuímos uma aceleração resultante, tal que:
Logo:

Passo 3
Agora que vem a malandragem, porque devemos lembrar lá das aulinhas de cálculo, sobre equações diferenciais ordinárias (EDO).
Saca só, a aceleração é simplesmente a derivada de segunda ordem do deslocamento , ou seja:
Sendo assim, se a gente pegar a equação que descobrimos no Passo 2, temos que:
Logo:
Dividindo tudo pela massa:
Agora, pra não ter que resolver a EDO (o que dá bastante trabalho) podemos, com toda malandragem do mundo, lembrar que a EDO que descreve o oscilador harmônico segue essa fórmula aqui:
Onde esse é a frequência angular. Ou seja, comparando com a equação que encontramos, temos:

Sendo assim, teremos que:
Passo 4
Portanto, agora vamos substituir os valores que a questão deu:
Mas essa é a frequência angular, pra achar a frequência de oscilação, usamos a equação:
Tal que:

Resposta
A frequência de oscilação é