Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 3.Problemas - Ex. 18
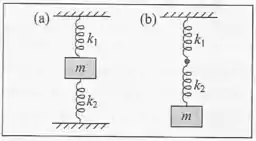
Com um bloco de massa e duas molas, de constantes elásticas e , montam-se dois arranjos indicados nas Figuras (a) e (b). Calcule as respectivas frequências angular e de pequenas oscilações verticais em torno do equilíbrio.
Passo 1
(a) Vamos começar pensando nas forças que agem sobre o primeiro bloco.
Onde definimos que a coordenada é positiva para baixo:
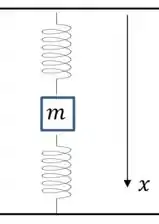
Então:
Essa é a equação de um oscilador harmônico com a seguinte frequência angular:
Passo 2
Quando as duas molas estão acopladas, a situação fica um pouco mais complicada. Vamos chamar de e os deslocamentos de cada uma delas:
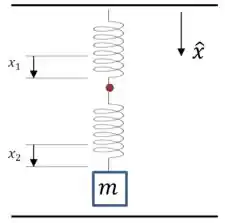
O deslocamento resultante do bloco vai ser dado pela soma desses dois deslocamentos:
E as forças devem ser iguais ao longo de toda a mola:
Além disso, pela lei de Hooke, temos que:
Onde é a constante elástica da mola resultante da junção das outras duas.
Substituindo essas últimas equações na primeira:
E usando o resultado da segunda equação:
Outra forma de escrever isso é:
Então a frequência angular nesse caso é:
Resposta
A frequências angulares são e .