Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 73
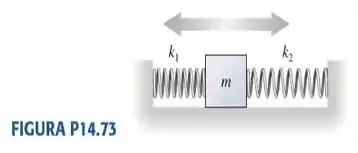
73. Sobre uma mesa sem atrito, um bloco está preso entre duas molas de constantes elásticas e , como mostra a FIGURA P14.73. Demonstre que a freqüência de oscilação do bloco é determinada por
onde e são as frequências com que ele oscilaria se estivesse preso somente à mola ou à mola .
Passo 1
Opa! Hey brother! Bora pra mais uma questãozinha sobre Ondulatória!
Se liga só! Pra entendermos melhor o nosso problema, bora fazer um diagrama de corpo livre com as forças que estão atuando no bloco.
E aqui está...
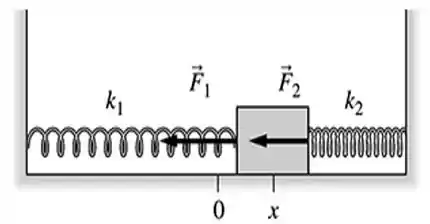
Bom! Por essa figura, podemos ver que as duas forças exercidas pela mola tem efeito restaurador, e apontando para a esquerda. No caso, o bloco deve estar se movendo para a direita.
Passo 2
Desse modo, fazendo o somatório das forças na direção horizontal com sentido positivo para direita, obtemos que...
Essas duas forças juntas tem como resultante uma força que chamaremos de , com mesmo sentido das outras. Isso acontece porque o significado da associação de molas nos diz que as duas molas podem ser substituídas por uma única mola cuja constante é a constante resultante da associação...
E o deslocamento dessa força resultante ; adivinha só!? É exatamente o mesmo deslocamento produzido pelas forças e . Sendo assim...
Passo 3
Desse modo, considerando como se houvesse uma única mola no sistema, bora usar a velha e conhecida fórmula da frequência, considerarando é claro, a constante de mola resultante ...
Como a frequência da mola é...
E a da mola é...
Então;
E voilà! Demonstração feita!