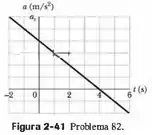
A Fig. 2-41 mostra a aceleração em função do tempo para uma partícula que se move ao longo do eixo . A escala vertical do gráfico é definida por . No instante , a velocidade da partícula é . Qual é a velocidade da partícula no instante ?

Inicialmente, é preciso prestar atenção que o gráfico é de uma reta, portanto, a aceleração tem função do tipo:

E como o gráfico intercepta no eixo quando , então conseguimos determinar a constante diretamente neste ponto.

Para determinar o valor da constante , vamos usar o ponto :

Isolando :

Com isso, definimos a função da aceleração:

Aplicando a definição explicitada no passo inicial, porém para esta questão, como não temos a velocidade , iremos usar o valor de . Assim:

Resolvendo esta integral, temos: