Exercícios de Regime Transitório, Permanente e Ressonância - Lista de Exercícios Resolvida
Questão 1
Considere um sistema massa-mola sujeito a uma força externa senoidal, com amplitude, frequência e constante de fase fixa. Marque a alternativa que descreve um procedimento para minimizar os efeitos de ressonância.
- Aumentar a constante de amortecimento do oscilador
- Diminuir a amplitude inicial do oscilador
- Garantir que o oscilador esteja inicialmente defasado em relação a força externa
- Trocar a mola para que a frequência natural do sistema seja igual à da força externa
- Diminui a constante de amortecimento do oscilador
Questão 2
Um sistema composto por um bloco de massa que se encontra na horizontal, sobre uma mesa, e que está ligada à parede por uma mola, tem seu movimento representado por:
Onde as constantes estão em unidades SI. Despreze o atrito do bloco com a superfície da mesa.
- Identifique a constante de amortecimento e a frequência angular na equação acima e determine o tipo de amortecimento sofrido pelo sistema.
- Dado que o bloco se encontra inicialmente na posição , onde a origem deste sistema corresponde à posição do bloco com a mola relaxada, e com velocidade inicial determine a equação horária do sistema em função de sua amplitude e fase inicial.
- Suponha agora que este sistema passe a oscilar sob a ação de uma força Ache a frequência angular sob qual a amplitude das oscilações é máxima. Assuma que o tempo é grande o suficiente para que a componente transiente do movimento já tenha sido totalmente suprimida. Encontre também esta amplitude máxima.
Questão 3
Considere o oscilador harmônico amortecido descrito pela equação diferencial
Qual a potência média fornecida pela força externa em uma oscilação?
Questão 4
Três osciladores têm freqüências angulares , onde é a frequência de uma força externa harmônica a eles aplicada. Sobre as respectivas amplitudes e , das oscilações no regime estacionário, podemos afirmar que:
- e
- e
Questão 5
Considere que um sistema massa-mola de frequência natural e coeficiente de amortecimento esteja submetido a uma força externa periódica de frequência . Após um intervalo de tempo suficientemente longo, podemos afirmar que o sistema massa-mola:
- Está em repouso definitivo
- Oscila com a frequência natural
- Oscila com a frequência da força externa
- Oscila com uma frequência múltipla inteira de
- Oscila com uma frequência igual a
- Executa um movimento caótico
Questão 6
Um corpo de oscila preso a uma mola que tem constante elástica igual a . A constante de amortecimento linear vale . O sistema é excitado por uma força senoidal de valor máximo igual a e frequência angular de . Qual é a amplitude das oscilações?
Questão 7
Um oscilador harmônico amortecido de frequência natural de oscilação , oscila sujeito a uma força externa periódica, da forma .Seu deslocamento em função do tempo durante dois minutos é exibido no gráfico abaixo. Julgue as afirmativas:
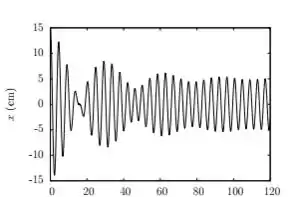
- O fenômeno de batimentos observado para indica a sobreposição de frequências diferentes. No entanto, uma das frequências é gradualmente atenuada pelo amortecimento.
- Após um intervalo de tempo suficientemente longo, o oscilador oscilará de forma periódica, com período:
- A partir de as forças de amortecimento cessam de agir no sistema.
- Em seu regime estacionário, a média de energia mecânica do oscilador sobre uma oscilação é conservada. No entanto, o mesmo não é verdade para a energia a cada instante.
- Apenas e estão corretas.
- Apenas e estão corretas.
- Apenas a esta incorreta.
- Apenas a esta incorreta.
Questão 8
Um bebê alegra-se gritando de felicidade e saltando para cima e para baixo em seu berço. Sua massa é de e o colchão do berço pode ser modelado como uma mola leve com constante de força de . Para que o movimento do bebê possua máxima amplitude, qual deve ser a frequência aplicada por ele ao colchão? (adote )
Questão 9
Um sistema massa-mola é imerso num meio viscoso, com constante de amortecimento e constante de mola . Uma força externa de frequência angular atua sobre a massa. Qual deve ser o valor da massa para que a amplitude do movimento seja máxima?
(a) 4 kg
(b) 35 g
(c) 40 g
(d) 350 g
(e) 35 kg
Ver solução completaQuestão 10
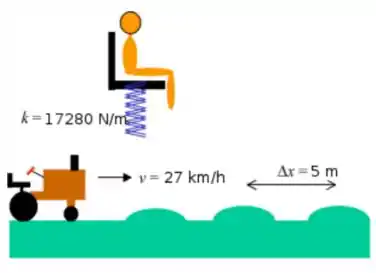
Considere um trator atravessando um campo onde existem ondulações em intervalos regulares. A distância entre cada monte é . Existe uma suspensão de mola ligada ao assento do motorista e este oscila em um regime no qual o amortecimento é desprezível. Podemos assumir uma mola de constante de mola , a massa do assento é e a do motorista é . O trator trafega a . Considere
- Qual a frequência com que o trator passa em cada elevação?
- Qual a frequência de oscilação natural do sistema assento-passageiro-mola?
- Se considerar que, durante o trajeto, a força máxima aplicada pelo trator sobre o sistema cadeira-motorista é de , qual a amplitude máxima do movimento de oscilação do motorista?(assuma que a força é harmônica).
- Para ocorrer o fenômeno de ressonância entre a força aplicada ao trator pelas ondulações e as oscilações sobre o sistema cadeira-passageiro, qual velocidade o trator deve atingir?(resposta em
Questão 11
Um oscilador amortecido tem frequência igual a daquela que teria () se sua constante de amortecimento fosse nula. Ao aplicarmos uma força externa cossenoidal, a frequência de ressonância (máxima amplitude) é (Dado: , .).
- 0, 8
- 1, 6
Questão 12
Um objeto de massa m se move no eixo sujeito a uma força horizontal de modo que a equação de movimento é dada por , onde ≥ 0, > 0 e > 0. A amplitude da solução particular desta equação varia com ω de acordo com o que mostra a figura em três situações correspondentes a valores diferentes e , tal que ≫ .
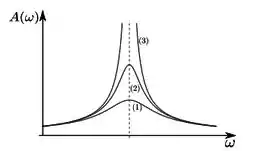
É INCORRETO afirmar que:
a) Quanto maior o valor de , maior a amplitude máxima da curva correspondente.
b) O amortecimento é maior na curva (1).
c) A frequência de ressonância é a mesma para as três curvas.
d) A curva (3) corresponde ao aso sem amortecimento.
e) Para ω ≫ , a solução particular é defasada de π em relação à força externa.
Ver solução completaQuestão 13
Na figura abaixo, os períodos dos regimes transitório e estacionário são:
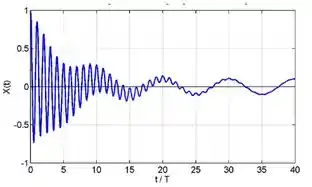
- e
- e
- e
- e
- e
Questão 14
Um sistema é formado por uma massa , uma mola de constante elástica e um amortecedor com constante de amortecimento . Se o sistema é sujeito a uma força externa , onde , a amplitude do sistema para baixíssimas frequências e na ressonância será, respectivamente:
Questão 15
Considere três osciladores fracamente amortecidos e forçados, que foram submetidos a uma força externa periódica de mesma amplitude. A partir do gráfico abaixo, é correto afirmar:
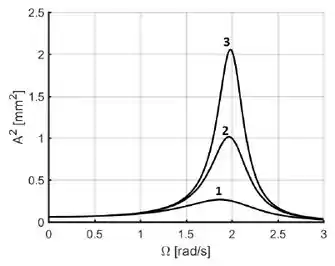
- nenhuma das demais alternativas
Questão 16
Observa-se que o ângulo entre um pêndulo simples e sua posição de equilíbrio varia da seguinte forma no tempo:
Onde o tempo está em segundos e o ângulo em radianos. Qual das afirrmações abaixo descreve melhor o sistema:
a) O pêndulo oscila livremente, sem atrito e sem força externa periódica;
b) O pêndulo está sofrendo uma força externa de frequência não sofre atrito;
c) O pêndulo está sofrendo uma força externa de frequência e não sofre atrito;
d) O pêndulo está sendo empurrado periodicamente com frequência igual à frequência de ressonância.
e) O pêndulo está sofrendo uma força de atrito e não sofre uma força externa periódica.
Ver solução completaQuestão 17
Considere um oscilador realizando um movimento harmônico simples (MHS). Assinale se as alternativas são verdadeiras ou falsas. Neste teste, CADA RESPOSTA ERRADA ANULA UMA CORRETA.
.[ ] O oscilador está sujeito a uma força impulsiva.
.[ ] A energia oscila entre as formas cinética e potencial.
.[ ] A presença de uma força externa gera uma ressonância quando a mesma tem frequência igual à frequência de oscilação livre.
.[ ] A presença de atrito não altera a frequência de oscilação mas apenas a amplitude.
.[ ] Em um MHS o deslocamento é descrito por uma função do tipo .
Ver solução completaQuestão 18
Cinco osciladores massa-mola, numerados de 1 a 5, estão suspensos no teto de uma sala. Uma britadeira cuja frequência de operação é fura o teto desta sala, forçando as massas a oscilarem. Os osciladores possuem todos a mesma massa e as constantes de mola têm os valores ; ; e . O oscilador que deve ter a maior amplitude de oscilação devido à perturbação externa é o:
a) oscilador 1
b) oscilador 2
c) oscilador 3
d) oscilador 4
e ) oscilador 5.
Ver solução completaQuestão 19
Considere as seguintes afirmações sobre oscilações forçadas amortecidas, quando a força é dada por F = F0 cos(t) e é a frequência natural das oscilações.
I. Para uma dada amplitude F0, a solução estacionária na frequência de ressonância pode ter amplitude no máximo igual a 4 vezes a amplitude de oscilação no limite .
II. Para , o sistema responde com uma baixa amplitude de oscilação.
III. No regime de amortecimento fraco e baixa frequência (), o movimento está em oposição de fase com a força externa.
Quais destas afirmações são corretas?
(a) Nenhuma.
(b) I, II e III.
(c) Apenas I e II.
(d) Apenas I e III.
(e) Apenas II e III.
(f) Apenas I.
(g) Apenas II.
(h) Apenas III.
Ver solução completaQuestão 20
Um bloco de 2 Kg está suspenso por uma mola e oscila verticalmente. Seu movimento é descrito pela equação . Observa-se que a amplitude do movimento se reduz a de seu valor inicial após 2 oscilações. Considerando que estas duas oscilações levam 2 s, determine:
a) O valor numérico dos coeficientes b e c e da constante elástica da mola.
b) Resolva a equação diferencial encontrando y(t) sabendo que o sistema inicia seu movimento na posição de equilíbrio e com velocidade = -12 m/s.
c) Considere agora que este oscilador seja acoplado à uma força externa e passe a oscilar conforme a equação . Encontre a frequência para a qual a amplitude da oscilação seja máxima e a amplitude do movimento para esta frequência. Considere que o tempo durante o qual o sistema está operando é grande o suficiente para que a parte homogênea já tenha decaído.
Ver solução completaQuestão 21
Após o regime transiente (passado um longo tempo), um oscilador amortecido forçado oscilará com
- A frequência da força externa
- A frequência do oscilador amortecido livre
- A frequência do oscilador não amortecido livre
- A frequência de batimento causada pela frequência do oscilador amortecido livre e a frequência da força externa.
- Nenhuma das respostas anteriores
Questão 22
Considere um bloco de m = 0, 5 kg, preso a uma mola de constante k = 50 N/m. O bloco pode movimentar-se sobre uma superfície horizontal em que um líquido viscoso foi derramado, dando origem a uma força dissipativa proporcional à velocidade, com constante . Uma força externa é aplicada ao bloco, onde e é uma freqüência angular sintonizável.
a) Calcule a potência média transferida pela força externa ao bloco, na situação estacionária, em função de .
b) Encontre a expressão exata da frequência em que essa potência média é máxima. Calcule o valor desta frequência, justificando as aproximações.
c) Suponha agora que a força externa é desligada, qual será a taxa de dissipação de energia do sistema?
Ver solução completaQuestão 23
Três osciladores têm freqüências angulares , onde é a frequência de uma força externa harmônica a eles aplicada. Sobre as respectivas amplitudes e , das oscilações no regime estacionário, podemos afirmar que:
- e
- e
Questão 24
No projeto de uma estrutura numa região propensa a terremotos, qual deve ser a relação entre a frequência da estrutura e a frequência típica de terremoto? A estrutura deve possuir amortecimento grande ou pequeno?
Ver solução completaQuestão 25
O gráfico abaixo representa o valor da amplitude (em metros) em função da razão entre a frequência angular de uma força periódica externa e a frequência angular de um oscilador harmônico. Sabendo-se que esta força atua sobre o oscilador, a partir da observação do gráfico abaixo, podemos afirmar que:
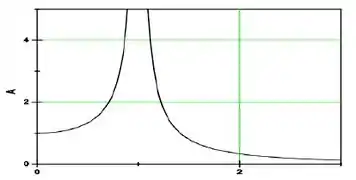
(a) O gráfico representa o comportamento de um sistema oscilatório forçado com amortecimento desprezível. Uma equação diferencial do tipo não é suficiente para analisar este movimento precisamente.
(b) O gráfico representa o comportamento de um sistema oscilatório forçado com amortecimento desprezível. Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.
(c) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento não desprezível, mas menor que . Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.
(d) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento não desprezível, mas menor que . Uma equação diferencial do tipo não é suficiente para analisar este movimento precisamente.
(e) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento forte e maior do que . Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.
Ver solução completaQuestão 26
A energia média de um oscilador fracamente amortecido, com coeficiente de amortecimento e frequência angular, cai a metade após dez oscilações completas. Consequentemente, a razão (fator de qualidade) vale:
- 5
Questão 27
Um oscilador harmônico de frequência angular natural de oscilação oscila na presença de uma força externa da forma e uma força dissipativa proporcional a sua velocidade Julgue as alternativas a seguir.
I No caso de haver ressonância, não realiza trabalho.
II No regime estacionário, a energia mecânica é constante em todo instante.
III A potência da força é negativa em todo instante.
IV No regime estacionário, a potência total é nula em cada instante.
V No regime estacionário, as potências médias de se cancelam.
- Apenas I e III estão corretas.
- Apenas II e V estão corretas.
- Apenas II e III estão corretas.
- Apenas I, II e IV estão corretas.
- Apenas III e V estão corretas.
Questão 28
Considere um oscilador amortecido e sujeito a uma força cossenoidal. As condições iniciais do oscilador podem
- Ampliar ou reduzir a amplitude nos instantes iniciais do movimento.
- Influenciam a amplitude do movimento mesmo em instantes muito posteriores ao início do movimento.
- Não têm qualquer influência sobre o movimento.
- Só podem aumentar a amplitude no início, pois o amortecimento reduzirá a amplitude de oscilação até o oscilador parar completamente.
- Só podem aumentar a amplitude no início, pois o amortecimento reduzirá a amplitude de oscilação até um valor constante não nulo.
Questão 29
Considere a equação da amplitude de oscilação do sistema mostrado na figura abaixo,
Onde é a amplitude constante de uma força oscilatória externa de frequência . Qual é a amplitude de oscilação e a velocidade máxima do objeto quando excitado na frequência de ressonância?
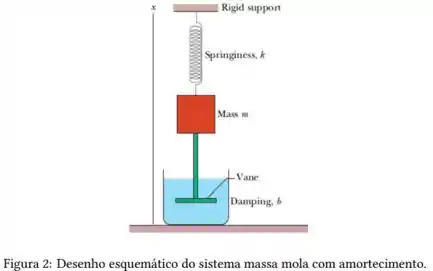
- e
- e
- e
- e
- e
Questão 30
A máxima amplitude de um oscilador simples formado por massa de , mola com constante de , e coeficiente de atrito de , ocorre quando submetido a uma força senoidal com frequência angular:
Ver solução completaQuestão 31
Seja um oscilador harmônico forçado, com amortecimento sub-crítico, onde e representam massa, constante de mola e coeficiente de atrito, respectivimente. A força externa é ligada em quando o oscilador está na posição e tem velocidade .
Tomando como a direção de vibração do oscilador, obtenha a partir do balanço das forças a equação do movimento (equação diferencial em , e ).
Encontre a solução transitória do movimento.
Deduza a solução estacionária do movimento, indicando amplitude e defasagem em relação à força externa aplicada.
Escreva a solução geral do movimento (transitória + estacionária) em termos das condições iniciais, e .
Ver solução completaQuestão 32
Um grupo de estudantes construiu um oscilador utilizando um bloco de massa e uma mola de constante elástica k. Um segundo grupo de estudantes construiu um outro oscilador acoplando um bloco de massa a uma mola idêntica àquela utilizada pelo primeiro grupo de estudantes. Os dois sistemas oscilam em um meio cuja força de resistência é proporcional à velocidade com o mesmo coeficiente de resistência . Cada grupo de estudantes aplicou uma força externa periódica de mesma amplitude aos sistemas. No regime estacionário, os valores máximos das potências médias dissipadas pelos osciladores em cada ciclo de oscilação, são dadas por e . Analisando a curva de ressonância abaixo, pode-se afirmar que:
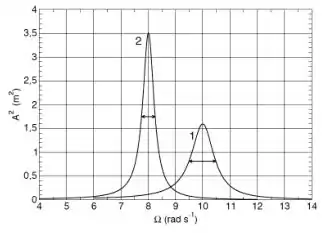
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 33
Um oscilador harmônico forçado é descrito por uma equação de movimento dada por:
![]()
O quadrado da amplitude de oscilação (normalizada pelo seu valor máximo) em função da frequência angular da força aplicada é dada pelo gráfico ao lado:
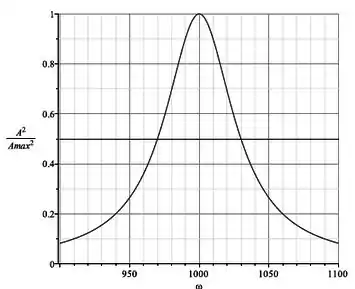
Se a massa do corpo é de 1 kg, responda:
a) Qual o valor da constante k da força de restauro?
b) Qual o valor da constante da força de restauro?
c) Se em um dado instante t = 0 a força externa for desligada, qual a função x(t) que descreve a posição da massa?
Ver solução completaQuestão 34
. Considere as seguintes afirmativas a respeito de um oscilador harmônico amortecido forçado:
. Uma vez atingido o regime estacionário, o trabalho médio da força externa resultante sobre o sistema é nulo.
. Quando o atrito sobre o oscilador é relativamente pequeno e a frequência da força externa sobre o oscilador harm��nico é igual a sua frequência natural a amplitude do movimento se anula.
. Quanto maior é a frequência da força externa sobre o oscilador, na média, mais energia por unidade de tempo é transferida ao sistema.
São VERDADEIRAS:
Ver solução completaQuestão 35
. Considere as seguintes afirmações:
- A frequência de um oscilador amortecido é sempre menor que a sua frequência natural.
- O amortecimento crítico é a condição em que uma partícula retorna ao equilíbrio com a maior rapidez, quando comparado com o amortecimento supercrítico.
- Um oscilador forçado, com coeficiente de amortecimento igual a zero , oscila com
a frequência da força motriz externa.
- Se a constante de amortecimento é nula , o oscilador harmônico forçado tem amplitude máxima , quando a frequência angular da força motriz e a frequência natural do oscilador são iguais, sendo o máximo valor da força motriz e a massa do oscilador.
- A solução geral do problema de um oscilador harmônico forçado é uma oscilação com a
frequência da força motriz externa.
- A altura da curva de ressonância da amplitude em função da frequência de um oscilador
harmônico amortecido e forçado aumenta com o aumento da constante de amortecimento .
- A largura da curva de ressonância da amplitude em função da frequência de um oscila-
dor harmônico amortecido e forçado aumenta com o aumento do coeficiente de amortecimento .
O número de afirmações corretas é:
Ver solução completaQuestão 36
Considere um sistema massa-mola sujeito a uma força externa senoidal, com amplitude, frequência e constante de fase fixa. Marque a alternativa que descreve um procedimento para minimizar os efeitos de ressonância.
- Aumentar a constante de amortecimento do oscilador
- Diminuir a amplitude inicial do oscilador
- Garantir que o oscilador esteja inicialmente defasado em relação a força externa
- Trocar a mola para que a frequência natural do sistema seja igual à da força externa
- Diminui a constante de amortecimento do oscilador
Questão 37
Um oscilador harmônico amortecido é formado por uma massa , uma mola de constatne elástica , e uma amortecedor com constante de . Ao aplicar uma força externa e , a amplitude do movimento será
- nenhuma das demais alternativas
- 10 mm
- 50 mm
- 100 mm
- 1 m
Questão 38
Um redutor de velocidades é feito com ondulações aproximadamente senoidais construídas na pista de uma rodovia. Deseja-se que a velocidade dos automóveis seja inferior a . Considere que a massa de um automóvel é de igualmente distribuída entre as rodas, e que os amortecedores independentes de cada roda têm uma mola de constante elástica mergulhada num fluido de viscosidade . O engenheiro decide que o redutor deve ser tal que o automóvel tenha a máxima amplitude de oscilação induzida pelas ondulações da pista exatamente quando o automóvel passa à velocidade pelo redutor.
Qual deve ser a distância entre as ondulações da pista?
Ver solução completa
Questão 39
A ponte pênsil Tacoma Narrows, localizada nos EUA, foi notícia há muitos anos, ela entrou em oscilação e segundos depois caiu, os engenheiros e geólogos da época estudaram as causas do desastre, facilmente foi constatado que a ponte caiu devido a um fenômeno físico denominado:

- Ressonância
- Compressão linear
- Dilatação
- Refração
- Reflexão
Questão 40
O gráfico abaixo mostra o quadrado da amplitude, , em função da frequência de oscilação de uma força senoidal aplicada. Dado que o sistema é fracamente amortecido, obtenha seu fator de qualidade, .
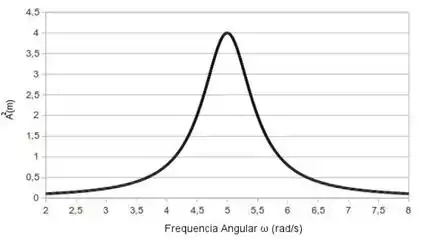
Questão 41
Considere um bloco de massa M preso à extremidade de uma mola de constante elástica k e comprimento relaxado e em repouso. A outra extremidade da mola é, então, presa a um dispositivo que oscila com frequência angular e cuja posição é dada por , onde a é uma constante positiva. Suponha que o bloco oscile com a mesma frequência do dispositivo e que o atrito seja desprezível.
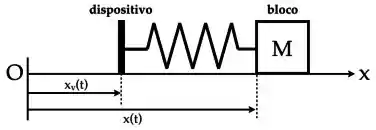
a) Desenhe o diagrama de forças que agem sobre o bloco de massa M e escreva as expressões para os vetores que representam tais forças de forma explícita num sistema de coordenadas apropriado.
(b) Deduza a equação diferencial que descreve o movimento do bloco em termos da variável .
(c) Resolva a equação diferencial encontrando a solução para as condições iniciais do problema.
(d) Qual a frequência do dispositivo para que o sistema entre em ressonância e o que ocorre com a amplitude neste valor de frequência?
Ver solução completaQuestão 42
Considere um sistema massa-mola sujeito a uma força externa senoidal, com amplitude, frequência e constante de fase fixas. Marque a alternativa que descreve um procedimento para minimizar os efeitos de ressonância.
(a) Aumentar a constante de amortecimento do oscilador.
(b) Diminuir a amplitude inicial do oscilador.
(c) Garantir que o oscilador esteja inicialmente defasado em relação à força externa.
(d) Trocar a mola para que a frequência natural do sistema seja igual à da força externa.
(e) Diminuir a constante de amortecimento do oscilador.
Ver solução completaQuestão 43
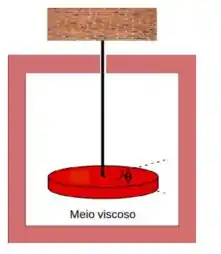
Um pêndulo de torção de massa , imerso em um meio viscoso, oscila em torno do seu ponto de equilíbrio obedecendo a seguinte equação de movimento:
Onde e .
- Determine a solução da equação do movimento considerando as seguintes restrições e
- Qual o tempo necessário para que a amplitude caia à metade?
- Calcule a amplitude da solução estacionária.
- Dadas as mesmas condições iniciais do ítem , qual o tempo necessário para que a amplitude da solução transiente seja da amplitude da solução estacionária?
Suponha agora que o pêndulo esteja sob a ação de um torque externo periódico
Questão 44
Considere um sistema massa mola de frequência natural e coeficiente de amortecimento esteja submetido a uma força externa periódica de frequência Após um intervalo de tempo suficientemente longo, podemos afirmar que o sistema massa-mola:
- Está em repouso definitivo.
- Oscila com frequência natural
- Oscila com a frequência da força externa
- Oscila com uma frequência múltipla inteira de
- Oscila com uma frequência igual a
- Executa um movimento caótico.