Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 29
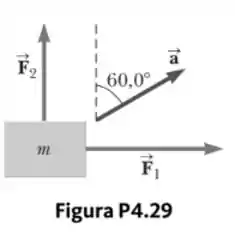
Observa-se que um corpo de massa tem uma aceleração com módulo de em direção a nordeste. A Figura P4.29 mostra o corpo visto de cima. A força que age sobre o corpo tem módulo de na direção norte. Determine o módulo e a direção da outra força horizontal que age sobre o corpo.
Passo 1
E aii galera, tudo bem com vocês?
Vamos fazer mais uma questão?
Vem comigo!
Vamos desenhar um diagrama para facilitar o entendimento:
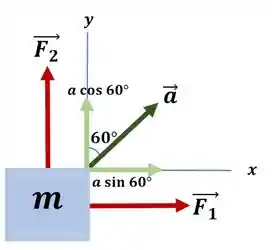
Para a aceleração:
Se :
Passo 2
Aplicando a segunda Lei de Newton:
Para que a equação de dois reitores seja igual, seus componentes devem ser iguais:
Resposta
Exercícios de Livros Relacionados
Propulsão solar. Um "iate solar'' é uma nave espacial com uma grande vela que é empurrada pela luz do Sol. Embora esse empurrão seja fraco em circunstâncias normais, pode ser suficiente para afastar a
A velocidade de uma partícula de 3,00k g é dada por v → = 8,00 t i ^ + 3,00 t 2 j ^m / s , com o tempo t em segundos. No instante em que a força resultante que age sobre a partícula tem um módulo de 3
Um balão de ar quente de massa M desce verticalmente com uma aceleração para baixo de módulo a . Que massa (lastro) deve ser jogada para fora para que o balão tenha uma aceleração para cima de módulo
A Fig. 5-45 mostra um bloco de 5,00k g sendo puxado em um piso sem atrito por uma corda que aplica uma força de módulo constante de 20,0N e um ângulo θ ( t ) que varia com o tempo. Quando o ângulo θ c
Três forças atuam sobre uma partícula que se move com velocidade constante v → = 2 m / s i ^ - 7 m / s j ^ . Duas das forças são F → 1 = 2N i ^ + 3N j ^ + - 2N k ^ e F → 2 = - 5N i ^ + 8N j ^ + - 2N k