Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 13
Uma onda transversal em uma corda possui amplitude de , comprimento de onda igual a e velocidade igual a . Ela é representada pela função dada no exercício 15.12.
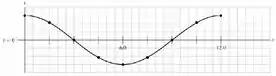
- Para o tempo , calcule para intervalos de iguais a (ou seja, e assim por diante) desde até . Faça um gráfico dos resultados obtidos. Essa é a forma da corda para o tempo .
- Repita o cálculo para os mesmos intervalos de para o tempo e para o tempo . Faça um gráfico da forma da corda para esses tempos. Qual é o sentido de propagação da corda?
Passo 1
Letra a)
A função de onda vai ser dada pela equação do exercício anterior, que é essa aqui ó:
E temos que , e . Assim a onda é descrita por:
Para temos:
Então, agora precisamos calcular para cada valor de . Os valores de são: . Jogando cada um desses valores no argumento do cosseno, podemos construir uma tabela com os valores correspondentes:
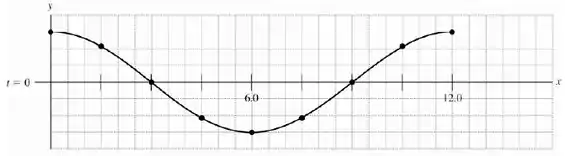
Podemos identificar um movimento oscilatório, pois temos que a posição vertical inicial é a mesma da posição vertical final. Colocando isso em um gráfico obtemos o seguinte resultado:
Passo 2
Letra b)
Agora precisamos calcular os mesmos pontos da função de onda, mas com e . Vamos calcular separadamente. Começando por :
E para os mesmos valores de , jogando na função e depois na calculadora, encontramos os seguintes valores de :
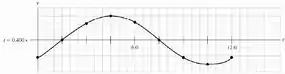
Podemos ver que aqui também temos um comprimento de onda inteiro, pois novamente as posições verticais iniciais e finais são iguais. No entanto, a onda se propagou no sentido , saca só como o gráfico fica:
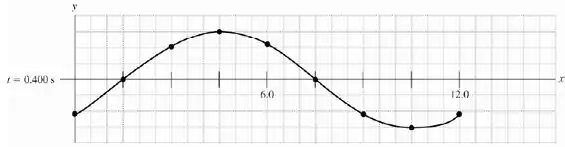
Passo 3
Certo? Agora vamos repetir o procedimento, mas fazendo :
E para os mesmos valores de , jogando na função e depois na calculadora, encontramos os seguintes valores de :
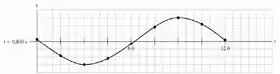
E o gráfico fica assim ó:
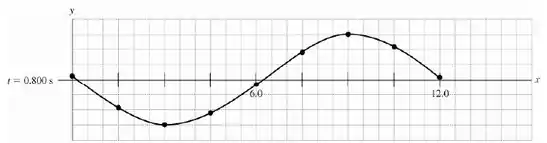
Comparando esses dois últimos gráficos, vemos que, comparando duas posições em , por exemplo, , no instante a onda está em uma posição abaixo do eixo , e num instante posterior, em , esse mesmo ponto está em cima do eixo . Portanto, concluímos que a onda se propaga no sentido .
Resposta
