Enunciado
Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 15.Exercícios - Ex. 43
Ondas em uma vareta. Uma vareta flexível de 2,0 m de comprimento não está presa, estando completamente livre para vibrar. Desenhe de modo claro essa vareta vibrando em seus primeiros três harmônicos, depois use seus desenhos para encontrar o comprimento de onda de cada um desses harmônicos. (Dica: as extremidades devem ser nós ou ventres?)
Passo 1
Falaii galerinha do Responde ai, tudo belezinha?
Para resolver este problema, devemos aplicar os conhecimentos sobre harmônicos de uma vareta vibrando e a identificação do comprimento de onda.
Os desenhos para os três primeiros harmônicos serão feitos por software. O segundo harmônico será o seguinte:
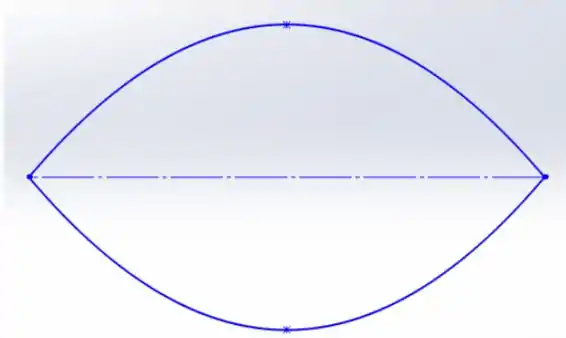
Passo 2
O comprimento L valerá do comprimento de onda, ou seja, como L é igual a 2,0m de comprimento, o comprimento de onda é igual a 4,0 m.
Portanto, o quarto harmônico será:
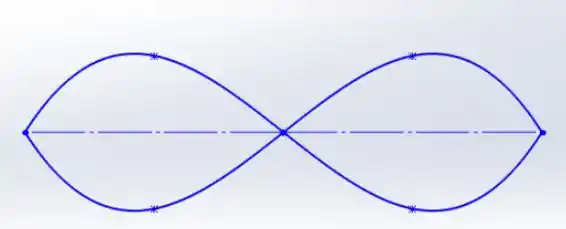
Passo 3
O comprimento L valerá do comprimento de onda, ou seja, como L é igual a 2,0m de comprimento, o comprimento de onda é igual a 2,0 m.
Portanto, o sexto harmônico será:
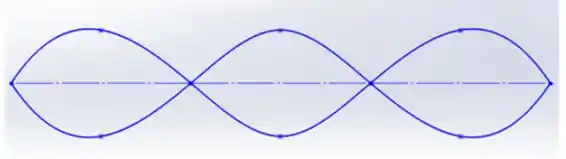
Passo 4
O comprimento L será igual a 3/2 do comprimento de onda, portanto, o comprimento de onda será igual a 1,33 m.
Portanto, conclui-se que os primeiros harmônicos dessa vareta são: o segundo, o quarto e o sexto e seus comprimentos de onda são 4,0 m, 2,0 m e 1,33 m respectivamente.
“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”
Resposta
Resposta nos passos.