Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 16.Exercícios - Ex. 25

Ondas sonoras estacionárias são produzidas em um tubo de comprimento igual a 1,20 m. Para o modo fundamental e os dois primeiros sobretons, determine a posição ao longo do tubo (medida a partir da extremidade esquerda) dos nós de deslocamento e dos nós de pressão supondo que (a) o tubo possui as duas extremidades abertas; (b) a extremidade esquerda do tubo está fechada e a direita está aberta.

Passo 1

Fala galera, bora lá!

Para resolver esse exercício devemos possuir o conhecimento sobre tubos sonoros que são instrumentos que permitem a vibração do ar, produzindo ondas sonoras com determinada frequência em seu interior. Eles podem ser classificados como abertos (com as duas extremidades do tubo abertas) ou fechados (com uma extremidade do tubo fechada).

Passo 2

Sendo considerado pelo exercício proposto um tubo de 1,2m de comprimento para ondas estacionárias no modo fundamental, devemos analisar para o caso do tubo ser aberto e para o caso do tubo fechado.

(a) Observe o tubo aberto a seguir ilustrado a seguir para o modo fundamental e os dois sobretons seguintes:

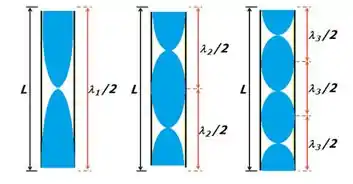
Passo 3

Podemos calcular os nós de deslocamento e os nós de pressão através das seguintes equações:

λ i = 2 L n

I p = λ i 2

n p = 0 ,   I p ,   2 I p ,   4 I p …

I d = L x

n d = I d ,   3 I d ,   5 I d …

Onde λ i é o comprimento de onda, L é o comprimento do tubo, I p é o intervalo entre os nós de pressão, n p é a localização dos nós de pressão, I d é o intervalo entre os nós de deslocamento, x é a quantidade de um quarto de comprimento de onda presente no interior do tubo e n d é a localização dos nós de deslocamento.

Passo 4

Assim sendo temos as seguintes posições para os nós de pressão e deslocamento, para o modo fundamental e os dois sobretons respectivamente:

Para i = 1

λ 1 = 2 1,2 1 = 2,4

I p = 2,4 2 = 1,2

n p = 0 ,   1 ,   2

I d = 1,2

n d = 0 ,   6

Para i = 2

λ 2 = 2 1,2 2 = 1,2

I p = 1,2 2 = 0,6

n p = 0 ;   0,6 ;   1,2

I d = 0,3

n d = 0,3 ; 0,9

Para i = 3

λ 3 = 2 1,2 3 = 0,8

I p = 0,8 2 = 0,4

n p = 0 ;   0,4 ;   0,8 ;   1,2

I d = 1,2 6

n d = 0,2 ; 0,6 ; 1

Passo 5

Assim temos para o estado fundamental, primeiro e segundo sobretom, em metros, respectivamente:

n d 1 = 0,6       n p 1 = 0 ;   1,2 n d 2 = 0,3 ; 0,9 ; 1       n p 2 = 0 ; 0,6 ; 1,2 n d 3 = 0,2 ; 0,6 ; 1       n p 3 = 0 ;   0,4 ;   0,8 ;   1,2

Passo 6

(b) Observe o tubo fechado a seguir ilustrado a seguir para o modo fundamental e os dois sobretons seguintes:

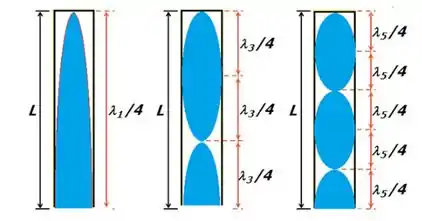
Podemos calcular os nós de deslocamento e os nós de pressão através das seguintes equações:

λ i = 4 L n

I p = λ i 4

n p = I p ,   3 I p ,   5 I p …

I d = L x

n d = 0 ,   2 I d ,   4 I d …

Passo 7

Assim sendo temos as seguintes posições para os nós de pressão e deslocamento, para o modo fundamental e os dois sobretons respectivamente:

Para i = 1

λ 1 = 4 1,2 1 = 4,8

I p = 4,8 4 = 1,2

n p = 1 , 2

I d = 1,2

n d = 0

Para i = 3

λ 3 = 4 1,2 3 = 1,6

I p = 1 , 6 4 = 0 , 4

n p = 0 ;   4 ;   1,2

I d = 0 , 4

n d = 0 ; 0 , 8

Para i = 5

λ 3 = 4 1,2 5 = 0,96

I p = 0,96 4 = 0 , 2 4

n p = 0 , 24 ;   0,72 ;   1,2

I d = 1,2 5 = 0,24

n d = 0 ;   0 , 48 ;   0 , 96

Assim temos para o estado fundamental, primeiro e segundo sobretom, em metros, respectivamente:

n d 1 = 0       n p 1 = 1,2 n d 3 = 0 ;   0,8       n p 3 = 0 , 4 ; 1,2 n d 5 = 0 ; 0,48 ; 0,96       n p 5 = 0 , 2 4 ;   0,72 ;   1,2

Resposta

  1. Assim temos para o estado fundamental, primeiro e segundo sobretom, em metros, respectivamente:

    2. n d 1 = 0,6       n p 1 = 0 ;   1,2 n d 2 = 0,3 ; 0,9 ; 1       n p 2 = 0 ; 0,6 ; 1,2 n d 3 = 0,2 ; 0,6 ; 1       n p 3 = 0 ;   0,4 ;   0,8 ;   1,2

  2. Assim temos para o estado fundamental, primeiro e segundo sobretom, em metros, respectivamente:

n d 1 = 0       n p 1 = 1,2 n d 3 = 0 ;   0,8       n p 3 = 0,4 ; 1,2 n d 5 = 0 ; 0,48 ; 0,96       n p 5 = 0,24 ;   0,72 ;   1,2

Exercícios de Livros Relacionados

Considere novamente a corda do problema 8 , com um extremo fixo e outro livre e de comprimento l . No instante t = 0 , um pequeno impulso de forma triangular está se propagando para a direita na corda
Uma corda vibrante de comprimento l , presa em ambas as extremidades, está vibrando em seu n -ésimo modo normal, com deslocamento transversal dado pela equação: y n x , t = b n sen ⁡ k n x cos ⁡ ω n t
Uma corda de comprimento l está distendida, com uma extremidade presa a um suporte e a outra extremidade livre. (a) Ache as frequências ν n dos modos normais de vibração da corda. (b) Desenhe a forma
O tubo de Kundt, que costumava ser empregado para medir a velocidade do som em gases, é um tubo de vidro que contém o gás, fechado numa extremidade por uma tampa M que se faz vibrar com frequência ν c
Que comprimento deve ter um tubo de órgão aberto num extremo e fechado no outro para produzir, como tom fundamental, a nota dó da escala média, ν = 262H z , a 15 ° C , quando a velocidade do som no ar