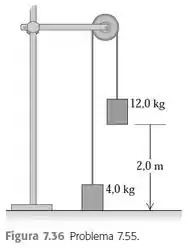
Passo 1
Oi, galerinha! Tudo bom? Aqui o enunciado já deu a dica que vamos usar o principio da conservação de energia para resolver! Então bora analisar a situação com calma.
O sistema é liberado do equilíbrio, então a energia cinética inicial é zero. A velocidade final da lata mais pesada vai ser igual a velocidade da outra lata, pois ambas se movimentam da mesma forma, já que estão conectadas por um mesmo cabo e estamos desconsiderando a resistência do ar.
Então quando a lata de chega ao chão, temos que somar a energia cinética mais a potencial das duas.
Bora lá!
Passo 2
Na situação inicial, quando o sistema é liberado temos apenas a energia potencial gravitacional da massa de :
Quando essa lata chega ao chão temos a energia cinética e a energia potencial da lata menor, e a energia cinética da lata maior:
Agora vamos aplicar o principio da conservação da energia!
Passo 3
Se a energia se conserva, então