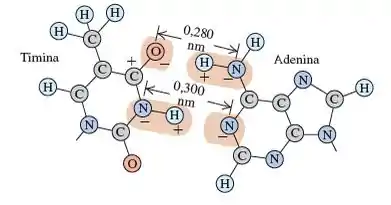
Pareamento de bases no DNA, I. Os dois lados da dupla hélice de DNA são ligados por pares de bases (adenina, timina, citosina e guanina). Em razão da forma geométrica dessas moléculas, a adenina se liga à timina e a citosina se liga à guanina. A Figura E21.21 mostra a ligação de timina e adenina. Cada carga na figura é , e a distância H—N é de .

(a) Calcule a força resultante que a timina exerce sobre a adenina. É uma força de atração ou repulsão? Para manter os cálculos simples, porém razoáveis, considere apenas as forças decorrentes das combinações de O—H—N e N—H—N, supondo que estas duas combinações sejam paralelas entre si. Lembre-se, no entanto, de que, no conjunto O—H—N, exerce uma força tanto sobre quanto , e de forma análoga o mesmo acontece no conjunto N—H—N.

(b) Calcule a força sobre o elétron no átomo de hidrogênio, que fica a de distância do próton. Em seguida, compare a intensidade da força de ligação do elétron no hidrogênio com a força de ligação das moléculas de adenina-timina.

Olá, tudo bem? Vou ajudar você aqui!

Letra (a):

Para calcular a força resultante da timina sobre a adenina precisamos primeiro identificar os pares de forças agindo: temos a força de atração de em com uma distância de , temos a força de repulsão de em a uma distância de . Temos também a força de repulsão entre dois a uma distância de . E por fim temos a força de atração de sobre o a uma distância de . Eu não contabilizei as forças de atração entre as cargas e , pois ambas cargas fazem parte da mesma molécula e não produzem força externa. Tranquilo?

Agora é somar todas essas quatro forças pra achar a resultante, borá fazer? Lembrando que as cargas são e que para fins de simplificação a gente vai admitir que as forças são paralelas, assim a força de atração vai ser positiva e a de repulsão, negativa.

A força resultante é de atração.