Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 12
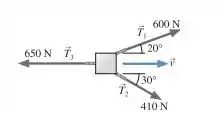
As três cordas que aparecem na vista aérea da FIGURA EX11.12 são usadas para arrastar um caixote por 3,0 m sobre um piso. Quanto trabalho é realizado por cada uma das três forças?
Passo 1
O trabalho de uma força constante é dado por:
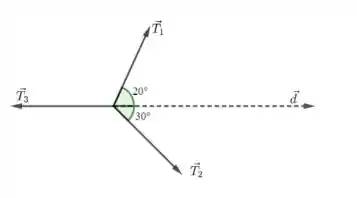
onde é o módulo da força, é o módulo do deslocamento e é o ângulo entre o vetor força e o vetor deslocamento. Veja no esquema a seguir as forças e os respectivos ângulos que elas fazem com o vetor deslocamento.
Passo 2
A primeira coisa que devemos nos atentar para esse exercício é o seguinte: para onde está apontando o vetor deslocamento? O vetor deslocamento aponta para a mesma direção e sentido do vetor velocidade. Assim, o vetor deslocamento está apontando horizontalmente para a direita. Notemos ainda que
- O ângulo entre e é ;
- O ângulo entre e é 30°;
- O ângulo entre e é 180° (mesma direção, sentidos opostos).
Passo 3
Como conhecemos o módulo de cada força, o deslocamento (= 3,0 m) e os respectivos ângulos, podemos calcular o trabalho:
Note que se você colocar corretamente os ângulos, não vai precisar ficar se preocupando com os sinais do trabalho: o sinal já sairá automaticamente no resultado final de suas contas! Legal, né?! :)
Resposta
1691 J; 1065 J; -1950 J.