Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 35
A partícula , de massa , está inicialmente posicionada no eixo x positivo, em , e sujeita a uma força repulsiva , exercida pela particula . A posição da partícula está fixa, na origem. A força é inversamente proporcional ao quadrado da distância entre as partículas, isto é, , onde é uma constante positiva. A partícula é largada do repouso e fica livre para se mover sob a influência da força, Encontre uma expressão para o trabalho realizado pela força sobre , como função de . Encontre a energia cinética e a rapidez de no limite em que tende a infinito.
Passo 1
Falaaa! Então ele está dizendo que a partícula sofre uma força que vem de , que empurra para longe de . está na origem e está na parte positiva de , em :
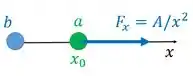
A gente quer o trabalho realizado por em função de se estiver livre para ser movida.
Como a força não é constante, vamos ter que recorrer às nossas amigas integrais. A fórmula do trabalho usando integrais é:
Sendo que é uma força na direção , é a posição inicial da partícula e é a posição final. Substituindo nossos dados:
Percebe que a gente fez . É como se a posição final da partícula fosse uma posição genérica . A gente faz isso para achar o trabalho em função de como ele pede.
Passo 2
Agora é calcular essa belezinha. Retirando o que é constante da integral:
Usando a regrinha de integrar polinômios:
Passo 3
Queremos agora a energia cinética e a rapidez da partícula quando .
Cara, falou de trabalho energia cinética no mesmo contexto, cê pensa logo no teorema do trabalho-energia cinética. Olha a expressão dele:
Isso diz que o trabalho total feito em uma partícula é igual à variação de energia cinética.
A energia cinética inicial é nula, pois a partícula parte do repouso:
Sobre a partícula só atua , então o trabalho total sobre ela é o que a gente calculou no passo anterior. Substituindo aqui:
Essa na verdade é a expressão da energia cinética no nosso ponto final genérico . Então vamos só mudar a notação para ficar fofo:
Passo 4
Mas quermos a energia cinética quando . Então vamos calcular esse limite:
Passo 5
Como a energia cinética é dada por
E quando , temos :
Podemos substituir isso em do passo anterior para achar :
Isolando o :
Resposta