Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 10
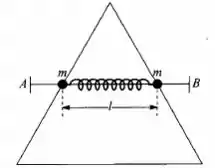
Uma estrutura rígida triangular é construída com três hastes iguais e seu plano é vertical, com a base horizontal. Nos dois outros lados estão enfiadas duas bolinhas idênticas de massa m, atravessadas por um arame rígido e leve AB, de modo que podem deslizar sobre as hastes com atrito desprezível, mantendo sempre o arame horizontal. As duas bolinhas também estão ligadas por uma mola leve de constante elástica k e comprimento relaxado . a) Mostre que uma expressão para a energia potencial do sistema em função do comprimento da mola é b) Para que valor de o sistema está em equilíbrio? c) Se soltamos o sistema na situação em que a mola está relaxada, qual é o maior valor de no movimento subsequente? d) Que tipo de movimento o sistema realiza no caso c) ?
Passo 1
- Vamos compor nossa energia potencial com a energia elástica e com a energia potencial gravitacional, ok? A gente já sabe que
- Se a gente for pensar em desenhar forças e componentes talvez fique complicado demais, então vamos lá simplificar essa parada. Já sabemos a força resultante desse sistema... Mas como? Vem comigo!
- Como sabemos que na posição do equilíbrio a mola está mais distendida que , ao soltarmos com velocidade nula ela vai se esticar, certo? E mesmo atingindo o equilíbrio de forças terá velocidade para continuar se esticando. Ou seja, a lógica aqui é calcular o momento em que sua velocidade de descida seja 0 e não a força resultante 0 ( atenção nisso hein, rs ). Em a mola vai subir de novo. Mas como a gente calcula isso? Chega junto!
- Galera, sabemos que nossa força é do tipo , portanto nosso sistema é oscilante como um sistema massa - mola comum, pois é descrito pelo mesmo tipo de equação. Ou seja, o movimento é do tipo harmônico simples.
Se quisermos achar a energia potencial gravitacional a gente precisa de um referencial onde será nosso potencial 0, dependendo de onder escolhermos isso vai nos dar a fórmula do enunciado ou não. Por isso que ele pede pra mostrar que é “uma” expressão e não “a” expressão do potencial.
Como a a energia potencial está negativa na fórmula vamos colocar nosso potencial 0 lá em cima, no topo do triângulo, fechou? Fica assim
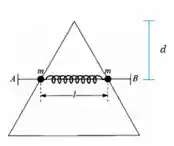
Só precisamos calcular agora a distância em função de , vamos dar um pulinho na trigonometria e notar que é a altura de um triângulo equilátero de base . Agora ficou mole né? Haha, fica assim
Passo 2
Se o problema quer o equilíbrio então
Passo 3
Se a velocidade inicial da mola é 0 e a final também, quer dizer que o trabalho resultante na mola foi de 0, wow! Pronto, agora que é só calcular quando .