Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 14

Um balde com água de 15,0   k g é suspenso por uma corda enrolada em torno de um sarilho, constituído por um cilindro sólido com diâmetro de 0,300   m e massa igual a 12,0   k g . O cilindro é pivotado sobre um eixo sem atrito passando em seu centro. O balde é libertado a partir do repouso no topo de um poço e cai 10,0   m até atingir a água. Despreze o peso da corda. a) Qual é a tensão na corda enquanto o balde está caindo? b) Com que velocidade o balde atinge a água? c) Qual é o tempo de queda? d) Enquanto o balde está caindo, qual é a força exercida pelo eixo sobre o cilindro?

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que um balde com água de 15,0   k g é suspenso por uma corda enrolada em torno de um sarilho, constituído por um cilindro sólido com diâmetro de 0,300   m e massa igual a 12,0   k g .

O enunciado ainda nos diz que o balde é libertado a partir do repouso no topo de um poço e cai 10,0   m até atingir a água.

Com essas informações, queremos encontrar a tensão na corda enquanto o balde está caindo, a velocidade na qual o balde atinge a água, o tempo de queda e a força exercida pelo eixo sobre o cilindro quando o balde está caindo.

Eita... muita coisa né???

Então vamos devagarinho responder cada uma das perguntas, combinadinho?? 😉

Passo 2

Oi, galerinha! Vamos com calma desenhando o diagrama de corpo livre para o balde para entender a situação:

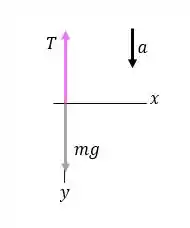
Vamos tomar como + y para baixo para facilitar as contas! Mas repara que a seta cinza representa o balde caindo e a seta rosa a tensão que sustenta ele.

No balde, vamos aplicar a segunda lei de Newton, no eixo vertical, ∑ F y = m a y , onde as forças estão atuando.

Agora vamos desenhar também um diagrama de corpo livre para o cilindro:

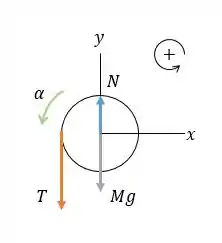
No clindro vamos aplicar a forma análoga da segunda lei de Newton, ∑ τ = I α , com direção em que o cilindro gira positivo. Lembra que essa força T , aqui em laranja, é a tensão que sustenta o balde.

Como as duas figuras estão conectadas, nós temos então que:

a b a l d e = R α c i l i n d r o

Agora vamos calcular!

Passo 3

  1. Então, para o balde:

    2. ∑ F y = m a y

    m g - T = m a

    E para o cilindro:

    ∑ τ = I α

    Como temos um cilindro,

    I = 1 2 M R 2

    Ficamos com,

    T R = 1 2 M R 2 α

    Substituindo ficamos com,

    m g - 1 2 M R α = m a

    Como α = a R então,

    m g - 1 2 M a = m a

    Isolando a ,

    a = m g m + M 2 = 15 k g 15 k g + 6 k g ⋅ 9,8 m / s 2 = 7 m / s 2

    Dessa forma,

    T = m g - a = 15 k g ⋅ ( 9,8 m / s 2 - 7 m / s 2 ) = 42 N

    Passo 4

  2. Agora, para analisar o movimento, vamos utilizar a equação de Torricelli, já que não nos pede e nem nos dá o tempo, t .

    3. v y 2 = v 0 y 2 + 2 a y ∆ y

    ⇒ v y = v 0 y 2 + 2 a y ∆ y

    v y = 0 + 2 ⋅ 7 m / s 2 ⋅ 10 m = 11,8 / m

    Passo 5

  3. Nós sabemos que: a y = 7 m / s 2 v 0 y = 0 ∆ y = 10 m

    4. E vamosa usar a equação:

    ∆ y = v 0 y t + a y t 2 2

    Para encontrar o tempo, t .

    ⇒ t = 2 ∆ y a y = 2 ⋅ 10 m 7 m / s 2 = 1,69 s

    Passo 6

  4. Aplicando a segunda lei de Newton no cilindro, temos que:

∑ F y = m a y

N - T - M g = 0

E então,

N = T + m g = 42 N + 12 k g ⋅ 9,8 m / s 2 = 160 N

Resposta

  1. T = 42 N
  2. v y = 11,8 / m
  3. t = 1,69 s
  4. N = 160 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29 . || Partindo do repouso, um C D de 12c m de que é diâmetro leva 3,0s para atingir sua velocidade normal de operação, que é de 2.000r p m . Considere que a aceleração angular seja constante. O mome
27 . || Uma bola de 1,0k g e outra, de 2,0k g , são ligadas por uma haste rígida e de massa desprezível com 1,0m de comprimento. A haste gira em sentido horário em torno de seu centro de massa a 20R P
Um satélite descreve a órbita elíptica mostrada. A única força exercida sobre o satélite é a atração gravitacional do planeta. O módulo da velocidade do satélite neste ponto é de 8.000 m/s.a. Algum to
11 . Considere o corpo na Figura PO 10.11 . Uma única força é exercida sobre ele. A linha de ação da força não passa pelo centro de massa do corpo. A aceleração do centro de massa do corpo em função d
12 . Um torque resultante constante é exercido sobre um corpo. Qual das grandezas seguintes não pode ser constante para o corpo? Escolha todas as alternativas aplicáveis. ( a ) posição angular ( b ) v