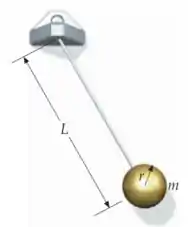
Um pêndulo físico consiste em uma bolinha de raio e massa suspensa de uma barra rígida de massa desprezíve, como na figura. A distância do centro de massa da bolinha ao ponto de suspensão é . Quando é muito menor do que , um pêndulo como este normalmente é tratado como um pêndulo simples de comprimento . (a) Mostre que o período para pequenas oscilações é dado por , onde é o período de um pêndulo simples de comprimento . (b) Mostre que, quando é menor do que , o período pode ser aproximado por . (c) Se e , determine o erro no valor calculado quando a aproximação é usada para o período. Qual deve ser o raio da bolinha para que o erro seja de por cento?

(a) Agora vamos substituir isso na fórmula do período e simplificar:

Vamos colocar em evidência na raiz quadrada, para nos aproximar da expressão que foi dada do enunciado:

E sabendo que :

Que é exatamente o que queríamos demonstrar.

(b) O que acontece com essa expressão quando ?

Nesse caso a fração dentro da raiz é menor do que , então podemos aplicar a expansão binomial como boa aproximação. Só para lembrar, essa expansão segue a seguinte fórmula:

Para chegar à expressão que foi dada no enunciado, vamos tomar apenas os termos até o primeiro grau (então excluímos tudo do em diante):

E então:

(c) Agora vamos comparar essa fórmula para com a aproximação do pêndulo simples. O erro dessa aproximação é o seguinte:

E no caso em que e :

Qual deve ser o raio da bolinha para que ?