Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.6 - Ex. 40

Um pequeno bloco apoiado sobre uma mesa horizontal sem atrito possui massa de 0,0250   k g . Ele está preso a uma corda sem massa que passa através de um buraco na superfície (Figura 10.48). No início, o bloco está girando a uma distância de 0,300   m do buraco com uma velocidade angular de 1,75   r a d / s . A seguir a corda é puxada por baixo, fazendo com que o raio do círculo se encurte para 0,150   m . O bloco pode ser considerado uma partícula.

a) O momento angular é conservado?

b) Qual é a nova velocidade angular?

c) Calcule a variação da energia cinética do bloco.

d) Qual foi o trabalho realizado ao puxar a corda?

Passo 1

Oi, galerinha! Tudo bom? O enunciado nos diz que um pequeno bloco (considere uma partícula) apoiado sobre uma mesa horizontal sem atrito possui massa de 0,0250   k g .

Ele está preso a uma corda sem massa que passa através de um buraco na superfície.

No início, o bloco está girando a uma distância de 0,300   m do buraco com uma velocidade angular de 1,75   r a d / s .

A seguir a corda é puxada por baixo, fazendo com que o raio do círculo se encurte para 0,150   m .

Queremos verificar se o momento angular é conservado, a nova velocidade angular, a variação da energia cinética do bloco e o trabalho realizado para puxar a corda...

Muita coisa né?? Então vamos devagarinho resolver cada uma!! 😉

Passo 2

Vamos analisar a situação. Há forças atuando sobre o sistema, sendo a normal N → , a peso P → e a tensão T → .

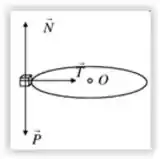
Repara que as forças normal e peso se anulam.

Logo, a força resultante é devida à tensão no cabo, que sempre atua na direção radial, de modo que o momento angular em relação ao furo é constante.

Portanto, variação do momento angular é zero. Ou seja, o momento é conservado.

Passo 3

Para responder a letra b, vamos lembrar que: as forças presentes no sistema produzem um momento angular resultante igual a zero, por isso, é conservado. Certo?

Feito isso é só igualarmos o momento inicial e final:

L 1 = I ω 1 e L 2 = I ω 2

m ω 1 r 1 2 = m ω 2 r 2 2  

Como pretendemos calcular a velocidade angular final, isolamos ω 2

ω 2 = ω 1 ( r 1 r 2 ) 2  

Substituindo a velocidade angular inicial e os raios; e resolvemos.

ω 2 = 1,75 r a d s ( 0,300   m 0,150   m ) 2

ω 2 =   1,75 r a d s ×   ( 0,045 ) 2

ω 2 =   1,75 r a d s ×   0,002025

ω 2 =   7,0   r a d s

Passo 4

Como o enunciado descreve, trata-se de um problema de energia cinética de rotação.

Lembramos que de início o bloco gira em torno de um eixo. Até aí tudo certo?! Pronto.

Observando a energia rotacional separadamente ao redor do eixo de rotação de um objeto, observa-se a seguinte dependência do momento de inércia do objeto, que traz a fórmula:

K = 1 2 I ω 2

E agora?

Já temos a solução! Trata-se de um problema com início e fim, que será quando o bloco passa pelo buraco. Portanto,

∆ K = K 2 - K 1

∆ K = 1 2 m ω 2 2 r 2 2 - 1 2 m ω 1 2 r 1 2

Para facilitarmos os cálculos, colocaremos em evidência a massa m ,

∆ K = 1 2 m ( ω 2 r 2 2 - ω 1 r 1 2 )

Prontinho! Agora é só resolver.

∆ K = 1 2 × 0,0250 ( 7,0 × 0,150 2 - 1,75 × 0,300 2 )

∆ K = 1 2 × 0,0250 × ( 0,826875 )

∆ K = 1 2 × 0,02067 = 1,03 × 10 - 2 J

Passo 5

No início deste problema, analisamos as forças utilizadas, a normal N → , a peso P → e a tensão T → , que produz um torque no sitema.

Assim, quando um torque realiza trabalho sobre um corpo rígido, a energia cinética varia de uma quantidade igual ao trabalho realizado.

W =   ∆ K

Como nenhuma outra força é aplicada ao longo do deslocamento, então 1,03 × 10 - 2 J de trabalho foram feitos para puxar o cabo.

Resposta

  1. O momento é conservado.
  2. ω 2 =   7,0   r a d s
  3. ∆ K = 1,03 × 10 - 2 J
  4. W = 1,03 × 10 - 2 J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 11-52 é uma vista de cima de uma barra fina homogênea, de comprimento 0,800m e massa M , girando horizontalmente a 20,0r a d / s , no sentido anti-horário, em torno de um eixo que passa pelo ce
A figura mostra uma visa de cima de um anel que pode girar em torno do centro como um carossel. O raio externo R 2 é 0,800m , o raio interno R 1 é R 2 / 2,00 , a massa M é 8,00k g e a massa da cruz no
No salto em distâcia, o atleta deixa o solo com um momento angular que tende a girar o corpo para a frente. Essa rotação, caso não seja controlada, impede que o atleta chegue ao solo com a postura cor
Uma roda de 0,250m de raio, que está se movendo inicialmente a 43,0m / s , rola 225m até parar. Calcule o módulo (a) da aceleração linear e (b) da aceleração angular da roda. (c) Se o momento de inérc
Uma bola maciça homogênea rola suavemente em um piso horizontal e depois começa a subir uma rampa com uma inclinação de 15,0 ° . A bola para momentaneamente após ter rolado 1,50m ao longo da rampa. Qu