O período de uma estrela variável pulsante pode ser estimado supondo que a estrela está executando pulsações longitudinais radiais no modo fundamental de uma onda estacionária, ou seja, que o raio da estrela varia periodicamente com o tempo, com um antinó do deslocamento na superfície da estrela. (a) Nesse modelo, o centro da estrela é um nó ou um antinó do deslocamento? (b) Por anologia com um tubo com uma extremidade aberta e a outra fechada, mostre que o período de pulsação é dado por , onde é o raio de equilíbrio da estrela e é a velocidade média do som no interior da estrela. (c) As estrelas anãs brancas típicas são feitas de uma substência com uma módulo de elasticidade volumétrico de e uma massa específica de e têm um raio igual a vezes o raio solar. Qual o período aproximado de pulsação de uma anã branca?

(b) O enunciado menciona que as pulsações ocorrem no modo fundamental.

Em uma corda, uma onda em modo fundamental contém meio comprimento de onda no comprimento da corda.

Analogamente, na estrela, a onda em modo fundamental contém meio comprimento de onda no diâmetro da estrela:

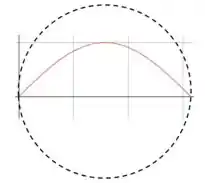
Podemos escrever isso da seguinte forma:

Lembrando da reção entre a frequência e o comprimento de onda, ficamos com:

E o inverso da frequência é justamente o período :

E essa é a fórmula que queríamos demosntrar.

(c) Vamos olhar de novo para a fórmula do período que acabamos de demonstrar:

E podemos reescrever a velocidade em termos do módulo de elasticidade volumétrico e da massa específica da estrela:

E o raio é vezes o raio do Sol, então: