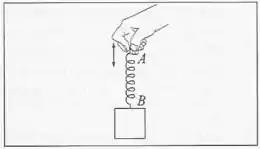
Uma pessoa está segurando uma extremidade de uma mola de massa desprezível e constante elástica . Na outra extremidade , há uma massa de suspensa, inicialmente em equilíbrio. No instante , a pessoa começa a sacudir a extremidade , fazendo-a oscilar harmonicamente com amplitude de e período de . (a) Calcule o deslocamente da massa em relação à posição de equilíbrio, para . (b) Calcule a força total exercida sobre a extremidade para .

Essa é uma EDO inomogênea, então sua solução geral vai ser da seguinte forma:

Onde é a solução da equação homogênea e é a solução particular. Vamos começar com a solução da homogênea:

Essa é a equação de um oscilador harmônico simples, e a solução já é bem conhecida:

E agora, para encontrar a solução particular, vamos olhar para essa equação:

O efeito da aceleração da gravidade é simplesmente de deslocar o equilíbrio mais para baixo.

Como queremos apenas as oscilações em torno do ponto de equilíbrio, podemos desconsiderar sem grandes problemas:

E então vamos chutar uma solução da seguinte forma:

Então nossa solução geral é:

Agora vamos aplicar as condições iniciais, começando por :

Então:

A outra condição inicial é . Primeiro temos que calcular a derivada:

E quando :

Então a nossa solução geral fica:

E a frequência natural é:

(b) Agora queremos calcular a força exercida sobre a extremidade .

Bom, a força transmitida ao longo da mola deve ser sempre a mesma. Lá em cima nós calculamos a força que ela realiza sobre o bloco:

A força que o bloco realiza sobre ela tem o mesmo módulo, mas sentido oposto:

E essa é a mesma força em todos os pontos da mola, inclusive na extremidade . Para escrever a força total só precisamos acrescentar o peso do bloco: