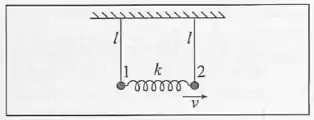
Dois pêndulos idênticos, formados por partículas de massa suspensas por barras de massa desprezível e comprimento , estão ligadas um ao outro por uma mola de massa desprezível e constante elástica , inicialmente relaxada, com os pêndulos na posição vertical de equilíbrio. Aplica-se à partícula uma força . (a) Obtenha a solução estacionária para os deslocamentos e das duas partículas. (b) Trace gráficos representando o andamento das amplitudes de oscilação das duas partícula em função de .
Passo 1
(a) Vamos começar montando EDOs para as coordenadas e de cada um dos pêndulos.
Para o pêndulo da esquerda, que não tem sofre a ação de nenhuma força externa:
E para o pêndulo da direita, só precisamos mudar o sinal da força da mola e acrescentar a força externa :
Cuidado para não confundir a frequência angular da mola com a frequência da força.
Ficamos então com um sistema de duas EDOs:
Passo 2
Agora vamos fazer aquela substituição que é tão comum para problemas de oscilações acopladas:
Somando as duas EDOs do sistema, ficamos com:
Que pode ser reescrita como:
E fazendo a segunda equação menos a primeira:
Que podemos reescrever como:
Então no final das contas ficamos com as seguintes equações:
Passo 3
Agora vamos resolver a primeira equação:
Vamos encontrar a solução particular (a solução estacionária que o enunciado pede), chutando que deve ter a seguinte forma:
Substituindo na EDO:
E o resultado é o mesmo para a segunda equação, só mudando de para :
Passo 4
Agora é só jogar isso tudo de volta em e :
Então:
Onde as frequências angulares são:
Passo 5
E o enunciado pede para traçarmos os gráficos que representem as amplitudes dessas partículas:
Vamos fixar todas as constantes no valor de uma unidade, apenas a frequência vai ser diferente:
Nesse caso, o gráfico da amplitude é:
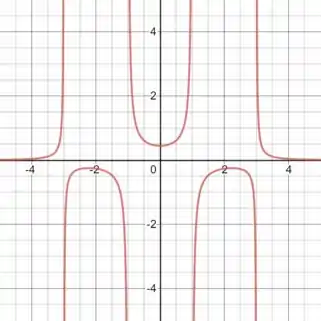
E para a amplitude :
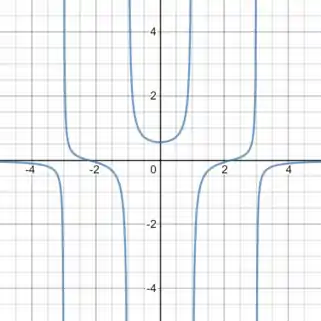
Resposta
Os deslocamentos são e , com e .