Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.5 - Ex. 57

Uma placa metálica fina de massa M tem forma retangular com lados a e b . Use o teorema dos eixos paralelos para determinar seu momento de inércia em relação a um eixo perpendicular ao plano da placa passando por um dos seus vértices.

Passo 1

Fala galera, tudo bem?

Para entender melhor a questão, vamos primeiro fazer um esboço da placa de lados a e b :

d e o momento de inércia, podemos aplicar o teorema dos eixos paralelos!

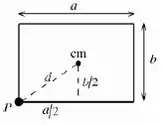
Tranquilo? Vamos começar?

Passo 2

Primeiro vou escolher o vértice inferior esquerdo para colocar o eixo perpendicular. Na figura ele está fincado no ponto P , saindo da tela.

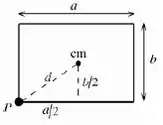
a / 2 em relação ao lado horizontal e b / 2 ao vertical, ok? Também é possível ver essas distâncias na imagem:

Onde c m é o centro de massa da placa.

A distância do eixo que passa pelo centro de massa até um dos vértices está indicada como d , e pelo teorema de Pitágoras temos:

d 2 = a 2 2 + b 2 2

d = a 2 2 + b 2 2

Tranquilo até aqui?

Passo 3

Agora precisamos saber a fórmula do momento de inercia de uma placa retangular. Olhando na tabela de momentos de inércia, temos que o momento de inércia do centro de massa de uma placa retangular é

I c m = M 12 ( a 2 + b 2 )

Agora podemos aplicar o teorema dos eixos paralelos!

Passo 4

Pelo teorema dos eixos paralelos temos que o momento de inércia de um objeto em relação a um eixo que passa a uma distância d do centro de massa é:

I = I c m + M d 2

Então agora é só substituir o que encontramos nos passos 2 e 3:

I = M 12 a 2 + b 2 + M 4 a 2 + b 2

I = a 2 + b 2 M 12 + M 4

I = a 2 + b 2 M + 3 M 12

I = a 2 + b 2 4 M 12

∴

I = M 3 ( a 2 + b 2 )

Beleza? O que achou? Responde Aí!

Resposta

M 3 ( a 2 + b 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pêndulo é constituído por uma esfera uniforme maciça com massa M e R raio suspensa pela extremidade de uma haste leve. A distância entre o ponto de suspensão na extremidade superior da haste e o ce
Considere um corpo rígido constituído por uma placa plana fina de forma arbitrária. Suponha que o corpo esteja sobre o plano xy e imagine que a origem seja um ponto O no interior ou no exterior do corp
O prato de discos de um fonógrafo antigo possui energia cinética igual a 0.0250 J quando gira com 45.0 rev/min. Qual é o momento de inércia do prato do fonógrafo em relação ao eixo de rotação?
Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Em relação à qual eixo uma esfera uniforme de madeira leve possui o mesmo momento de inércia de uma casca cilíndrica de chumbo de mesma massa e raio em relação a um diâmetro?