Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.5 - Ex. 58
a) Para a placa retangular fina indicada na parte (d) da Tabela 9.2, ache o momento de inércia em relação a um eixo situado sobre o plano da placa passando pelo seu centro e paralelo ao eixo indicado na figura.
b) Ache o momento de inércia da placa em relação a um eixo situado sobre o plano da placa passando pelo seu centro e perpendicular ao eixo mencionado no item (a).
Passo 1
Oi, galerinha! Tudo bom?
O enunciado fala para usarmos a placa da tabela. Ela é essa aqui
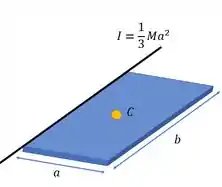
Repara que ele nos dá o momento de inércia em relação ao eixo que passa pela borda dessa placa.
E ele pede o momento de inércia em relação a um eixo paralelo a esse que está na figura e que esteja no plano da placa, passando pelo centro dela . Ou seja, passando por seu centro de massa. Podemos chama-lo de eixo :
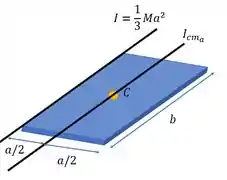
Como a gente já tem o momento de inércia em relação a um eixo e queremos achar o momento de inércia em relação a um eixo paralelo ao primeiro que passa pelo da figura, a gente pode usar o teorema dos eixos paralelos.
Onde, é a massa da placa. E é a distância entre os eixos paralelos.
Bora lá!
Passo 2
a) Como queremos o momento de inércia que passa pelo centro de massa
Sendo que segundo a tabela,
Vemos pela figura que a distancia entre os eixos vale
Logo:
Tranquilo até aqui?
Passo 3
b) Nessa vamos fazer algo muito parecido. Mas a gente pode entender pela geometria da placa que o momento de inércia em relação a um eixo paralelo ao seu segmento que vale e que está na borda da placa é
Aí ele nos pede para achar o momento de inércia em relação a um eixo que passa pelo da placa, mas esse eixo é perpendicular ao eixo do item anterior. Temos:
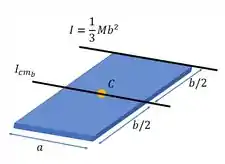
Temos a mesma situação do item anterior agora. A gente pode usar o teorema dos eixos paralelos.
Show?
Passo 4
Como queremos o momento de inércia que passa pelo centro de massa
Sendo que
E agora a distancia vai valer,
Logo:
E aí! entendeu tudo? Responde Aí!
