Uma placa retangular uniforme com largura , altura e peso está suspensa com seus lados superior e inferior na horizontal (figura ). No canto inferior esquerdo, há uma dobradiça, e no canto superior direito há um cabo. a) Para qual ângulo com a vertical a tensão no cabo será mínima, e qual é essa tensão? b) Sob as condições do item (a), ache os componentes horizontal e vertical da força que a dobradiça exerce sobre a placa.

Passo 1
Faaala galeraa, bora fazer mais uma questão?
O enunciado pediu pra gente encontrar (a) o valor do ângulo que faz o tensão no cabo ser mínima, o valor dessa tensão e (b) as componentes horizontal e vertical da força que a dobradiça exerce sobre a placa.
Vamos esboçar o diagrama de corpo livre da placa para entender melhor isso:
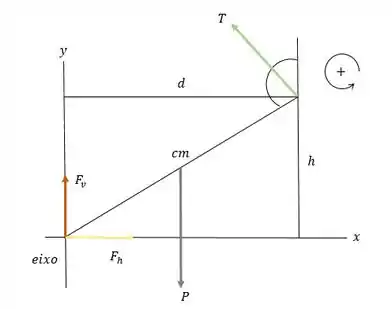
Observe que é o centro de massa da placa ali representado, que está sujeito a uma força peso . Temos a tensão no cabo de sustentação e as componentes de força e no eixo da dobradiça.
A tensão mínima ocorre quando o cabo é perpendicular ao braço de alavanca, dessa forma, temos e o torque será dado por:
Além disso, para a força (de tensão no cabo), podemos usar as relações do trângulo retângulo formado na nossa figura:
Sendo assim, o que nós vamos fazer é usar as equações de equilíbrio () para obter o valor da tensão e das componentes e em função das dimensões da nossa placa.
Vamos lá!
Passo 2
a) Então, fazendo:
Vamos ter o somatório dos torques no canto superior direito da placa:
é negativo para e nesse caso:
Então,
Assim, substituindo o ângulo na nossa equação de equilíbrio e isolando , vamos ter:
Passo 3
b) Agora aplicando , temos que:
Mas vimos no passo anterior que , então substituindo, temos:
E encontramos a componente horizontal da força :
De maneira semelhante, aplicando , temos que:
E substituindo a expressão da tensão encontrada, temos:
E encontramos nossa componente vertical:
Valeu, galera! Até a próxima! 😉