Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 12

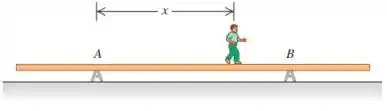
Uma viga de alumínio uniforme com 9,0 m de comprimento e peso de 300 N repousa simetricamente sobre dois suportes separados por uma distância de 5,0 m (Figura 11.25). Um adolescente pesando 600 N parte do ponto A e caminha para a direita. a) Em um mesmo diagrama, construa dois gráficos mostrando as forças de baixo para cima FA e FB exercidas sobre a viga nos pontos A e B, em função da coordenada x do adolescente. Seja 1 cm = 100 N na escala vertical e 1 cm = 1,0 m na escala horizontal. b) Pelo seu diagrama, até que distância à direita do ponto B ele pode caminhar sem que a viga tombe? c) Qual será a distância máxima até a extremidade direita da viga em que o ponto de suporte B pode ser colocado para que o adolescente possa atingir essa extremidade sem que comece a tombar?

Passo 1

O enunciado nos diz as características de uma viga onde uma pessoa anda de um ponto A até B:

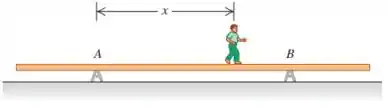
A viga tem 9 m de comprimento e pesa 300   N sobre dois suportes (os pontos A e B) separados por 5 m .

Queremos plotar dois gráficos mostrando as forças de baixo para cima F A e F B exercidas sobre a viga nos pontos A e B, em função da coordenada x do adolescente.

Com esse gráfico, queremos saber até que distância à direita do ponto B ele pode caminhar sem que a viga tombe.

Por fim, queremos calcular a distância máxima até a extremidade direita da viga em que o ponto de suporte B pode ser colocado para que o adolescente possa atingir essa extremidade sem que comece a tombar.

Para resolver o problema usaremos as relações de torque e de equilíbrio de corpo rígido, sendo essas a somatória das forças agindo em todos os pontos do sistema.

Passo 2

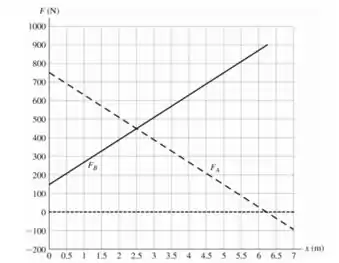
  1. Nosso gráfico fica da seguinte forma:

    2. Passo 3

  2. De acordo com o diagrama, é possível caminhar até 6.25   m , ou 1.25   m depois do ponto B.

    3. A partir desse ponto a força sentida no ponto A será zero, assim não estando mais em contato com o ponto e podendo tombar.

    Passo 4

  3. Temos que pelo torque calculando com base na distância do ponto B do fim da viga, temos que a soma dos torques tem que ser igual a 0.

Logo, pegando o valor de F b na extremidade e de F a em outro ponto, teremos:

d = F a ⋅ d F b = 200   N ⋅ 4.50   m 900   N = 1.00   m

Resposta

b) 1.25   m   d e p o i s   d o   p o n t o   B

c) 1.00   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas pessoas transportam uma prancha de madeira uniforme com 3,0 m de comprimento e peso de 160 N. Se uma das pessoas aplica em uma extremidade uma força de baixo para cimade 60 N, em qual ponto a out
Uma escada uniforme de 5,0m de comprimento repousa contra uma parede vertical sem atrito e sua extremidade inferior está situada a 3,0m da parede. A escada pesa 160N . O coeficiente de atrito estático
Determine a tensão T em cada cabo e o módulo, a direção e o sentido da força exercida sobre a viga pelo pivô em cada um dos arranjos indicados na Figura 11.26. Em cada caso, seja p o peso da caixa sus
Em um jardim zoológico, uma barra uniforme de 3,0 m de comprimento e 240 N é mantida em posição horizontal por meio de duas cordas amarradas em suas extremidades (Figura 11.30). A corda da esquerda fa
Uma porta de 1,0 m de largura e 2,0 m de altura pesa 280 N e é suportada por duas dobradiças, uma situada a 0,50 m a partir do topo e a outra a 0,50 m a partir do ponto inferior. Cada dobradiça suport