Arcobotante. a) Um edifício simétrico possui um telhado com inclinação de baixo para cima formando um ângulo de 35,0º acima da horizontal em cada lado. Se cada lado do telhado uniforme pesa 10000 N, ache a força horizontal que esse telhado exerce no topo da parede, que tende a empurrar as paredes para fora. Que tipo de prédio correria maior risco de desabamento: um com paredes altas ou outro com paredes baixas? Explique.

b) Como você verificou no item (a), as paredes altas correm o risco de desabar com o peso do telhado. Esse problema preocupou os construtores de grandes estruturas no passado. Uma solução usada nas grandes catedrais góticas nos anos de 1200 foi o arcobotante, um suporte de pedra entre as paredes e o solo que ajudava a conter as paredes. Uma igreja gótica possui um telhado uniforme que pesa um total de 20000 N e se ergue a 40º do plano horizontal em cada parede. As paredes têm 40 m de altura e um arcobotante encontra cada parede 10 m abaixo da base do telhado. Que força horizontal essa estrutura deve aplicar à parede?

Porque um prédio fica equilibrado? Os movimentos de rotação e translação se anulam, há forças atuantes sobre ele e uma delas é a do Torque. Então para isso temos .

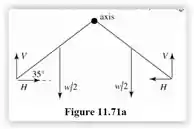
V e H são a vertical e forças horizontais que cada parede exerce sobre o telhado. é o total peso do telhado.

Aplicamos o torque à metade do telhado, com o eixo ao longo da linha onde as duas metades se juntam. Vamos considerar que cada metade tenha um comprimento L.

Assim, vai ficar

Como , então

Pela terceira lei de Newton, o teto exerce uma força horizontal e externa na parede. Se um torque for aplicado sobre o chão, essa força será maior e portanto, afeta as paredes mais altas.