Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.5 - Ex. 47
Um poço com paredes verticais e água no fundo ressoa em e em nenhuma outra frequência mais baixa. (A parte do poço cheia de ar se comporta como um tubo com uma extremidade aberta e outra fechada) O ar no interior do poço tem uma massa específica de e um módulo de elasticidade volumétrico de . A que profundidade está a superfície da água?
Passo 1
Vamos pensar no perfil harmônico de um tubo fechado (em uma das extremidades).
A fórmula que relaciona a frequência com seu harmônico é
Dá uma olhada no desenho que fica mais claro:
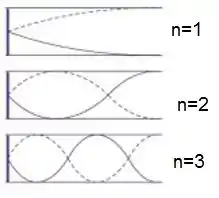
Como a frequência fundamental é a mais baixa de todas frequências admitidas pelo poço, temos que . A profundidade da água coincide com o tamanho do poço, que vou chamar de . Mas para determinar , precisamos saber com qual velocidade essa onda se propaga no poço.
Passo 2
O problema nos dá a densidade do ar () e o módulo da elasticidade volumétrica () dentro do poço, e com esses dados podemos calcular a velocidade de propagação:
Passo 3
Sabendo a frequência fundamental e a velocidade podemos então calcular o tamanho o tubo :
Assim chegamos ao valor de para a profundidade da superfície da água.