Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.5 - Ex. 46

O tubo , que tem de comprimento e duas extremidades abertas, oscila na terceira frequência harmônica. Está cheio de ar, no qual a velocidade do som é .O tubo , com uma das extremidades abertas, oscila na segunda frequência harmônica. A frequência de oscilação de coicide com a de . Um eixo coincide com o eixo do tubo , com na extremidade fechada. Quantos nós existem no eixo ? Qual é o menor e o segundo menor valor da coordenada desses nós? Qual é a frequência fundamental do tubo ?

Passo 1

Vamos pensar no segundo harmônico de um tubo fechado (em uma das extremidades).

A fórmula que relaciona a frequência com seu harmônico é

Dá uma olhada no desenho que fica mais claro:

Na frequência fundamental temos nó, e num total de um quarto de comprimento de onda. Na segunda frequência harmônica () observamos nós e um total de de comprimento de onda.

Na terceira frequência harmônica () observamos nós e um total de de comprimento de onda.

Então, como queremos analisar o segundo harmônico, temos .

Passo 2

O menor valor é justamente na extremidade fechada, que coincide com a origem do eixo , ou seja em .

Passo 3

Para determinar o segundo menor valor, precisamos primeiro saber o tamanho do tubo (vamos chamar de ).

Sabendo que e que é aberto e que é fechado:

Como a velocidade do som é a mesma nos dois tubos, podemos cancelar dos dois lados. Fazendo as continhas ficamos com:

Passo 4

Como sabemos que o segundo harmônico corresponde a , então temos:

Agora que sabemos o comprimento de onda vamos olhar de novo para o desenho lá do passo .

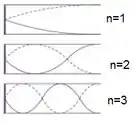
Podemos ver aqui na direita que o segundo nó do segundo harmônico corresponde a meio comprimento de onda. Assim, se um comprimento de onda inteiro é , o valor que queremos é a metade disso.

Ou seja, o segundo menor valos de vai ser em

Passo 5

A frequência fundamental no tubo vai ser dada por:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corda de comprimento l está distendida, com uma extremidade presa a um suporte e a outra extremidade livre. (a) Ache as frequências ν n dos modos normais de vibração da corda. (b) Desenhe a forma

O tubo de Kundt, que costumava ser empregado para medir a velocidade do som em gases, é um tubo de vidro que contém o gás, fechado numa extremidade por uma tampa M que se faz vibrar com frequência ν c

Que comprimento deve ter um tubo de órgão aberto num extremo e fechado no outro para produzir, como tom fundamental, a nota dó da escala média, ν = 262H z , a 15 ° C , quando a velocidade do som no ar

Uma onda sonora plana monocromática de pressão dada por p i = ℘ cos ⁡ - k x x + k y y - ω t onde k 2 = k x 2 + k y 2 + k z 2 = ω 2 / v 2 ( v = velocidade do som), incide com ângulo de incidência θ 1 ,

(a) Mostre que, para uma onda sonora harmônica de frequência angular ω , em três dimensões, num fluido cuja densidade de equilíbrio é ρ 0 , o deslocamento u → (que neste caso é um vetor!) está relacio