Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 95

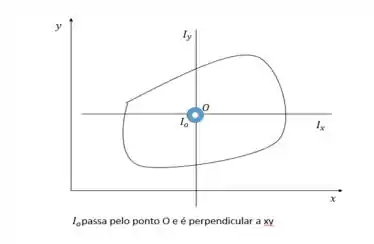
Considere um corpo rígido constituído por uma placa plana fina de forma arbitrária. Suponha que o corpo esteja sobre o plano xy e imagine que a origem seja um ponto O no interior ou no exterior do corpo. Seja Ix o momento de inércia em relação ao eixo Ox, Iy o momento de inércia em relação ao eixo Oy e IO o momento de inércia do corpo em relação a um eixo perpendicular ao plano e passando pelo ponto O. a) Considerando elementos de massa mi com coordenadas (xi, yi), mostre que I o = I x + I y . Essa relação é o teorema dos eixos perpendiculares. Note que o ponto O não precisa ser o centro de massa. b) Para uma arruela fina de massa M, raio interno R1 e raio externo R2, use o teorema dos eixos perpendiculares para achar o momento de inércia em relação a um eixo situado no plano da arruela e que passa através de seu centro. Você pode usar as informações da Tabela 9.2. c) Use o teorema dos eixos perpendiculares para mostrar que o momento de inércia de uma placa fina quadrada de massa M e lado L em relação a qualquer eixo situado no plano da placa e que passa através de seu centro é igual a ML2. Você pode usar as informações da Tabela 9.2.

Passo 1

O exercício nos fala sobre uma placa fina sendo girada de várias maneiras diferentes com momentos de inércia diferentes atrelado para cada eixo que é tomado como referência. Nos é pedido para demonstrar o teorema dos eixos perpendiculares usando as relações dos momentos de inércia conhecidos. Nas alternativas b) e c) precisamos encontrar o valor do momento de inércia utilizando o teorema dos eixos paralelos.

Passo 2

  1. Temos que a relação para o momento de inércia é dada da seguinte forma:

    2. I = ∑ i m i ⋅ r i 2

    onde r i 2 = x i 2 + y i 2   e i é o índice da quantidade de coordenadas do sistema, que no nosso caso serão só duas, logo i irá até 2.

    Nos é dado que I o =   ∑ i m i ⋅ r i 2 =   ∑ i m i ⋅ x i 2 + y i 2 =   ∑ i m i ⋅ x i 2 + ∑ i m i ⋅ y i 2

    Usando a definição novamente, temos que I x = ∑ i m i ⋅ x i 2 e I y = ∑ i m i ⋅ y i 2 . Assim, temos que I o será:

    I o = I x + I y

    Passo 3

  2. Temos que o momento de inércia do objeto dado, pela tabela que é sugerida, é I x = 1 4 ⋅ M ⋅ ( R 1 2 + R 2 2 ) . Pela simetria do problema, tanto o momento de inércia no eixo Ox quanto pelo eixo Oy são iguais. Assim I x = I y , logo, pelo teorema dos eixos paralelos, teremos que

    3. I o = I x + I y = 1 4 ⋅ M ⋅ R 1 2 + R 2 2 +   1 4 ⋅ M ⋅ R 1 2 + R 2 2 = 1 2 ⋅ M ⋅ R 1 2 + R 2 2

    Passo 4

  3. Usando o mesmo raciocínio da alternativa anterior, temos a mesma questão de proporcionalidade, onde I x = I y , e I x = 1 12 ⋅ M ⋅ L 2 . Usando o teorema dos eixos paralelos, teremos que:

I o = I x + I y = 1 12 ⋅ M ⋅ L 2 + 1 12 ⋅ M ⋅ L 2 = 1 6 ⋅ M ⋅ L 2

Resposta

b) 1 2 ⋅ M ⋅ R 1 2 + R 2 2

c) 1 6 ⋅ M ⋅ L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia da área da seção transversal da viga em relação ao eixo y .
Determine a intensidade e o sentido direcional da força em A em relação ao ponto P .
Determine o momento de inércia I x da área sombreada em relação ao eixo y .
Determine o momento de inércia I x da área sombreada em relação ao eixo x .
66. Determine o produto de inércia da área da seção transversal em relação aos eixos u e v .