Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 18

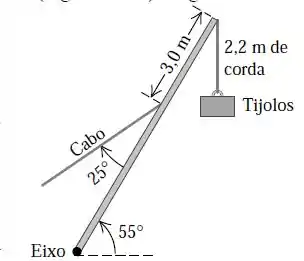
Um guindaste de 15000   N gira em torno de um eixo livre de atrito na sua base e está suportado por um cabo que forma um ângulo de 25 ° com o guindaste (Figura 11.29). O guindaste tem 16   m de comprimento e não é homogêneo; seu centro de gravidade está a 7,0   m do eixo, medido ao longo do guindaste. O cabo está preso a 3,0   m da extremidade superior do guindaste. Quando o guindaste é erguido a 55 ° acima do plano horizontal sustentando um palete de tijolos pesando 11000   N por uma corda leve de 2,2   m , ache a) a tensão no cabo e b) os componentes horizontal e vertical da força que o eixo exerce sobre o guindaste. Comece com um diagrama do corpo livre para o guindaste.

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

Pelo enunciado temos que o guindaste sustenta os tijolos e é ajudado por um cabo. Como o sistema está em repouso, vamos aplicar as condições de equilíbrio ao guindaste. Mas primeiro, vamos desenhar o diagrama de corpo livre para entender as forças que está atuando ali, tal que:

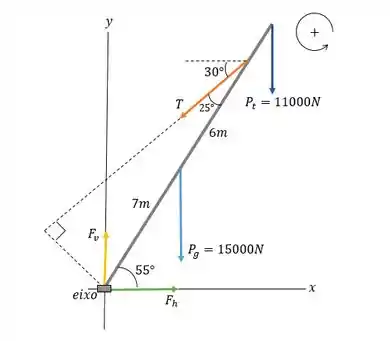
F h e F v são os componentes da força exercida pelo eixo. T →   puxa para a esquerda, então F h está para a direita. T →   também puxa para baixo e os dois pesos são para baixo, então F v é para cima. Sabendo disso, bora lá ver se essa questão é isso tudo mesmo...

Passo 2

a) Belezoca, aplicando o equilíbrio dos torques:

∑ τ = 0

Temos que:

T ( [ 13   m ] ⋅ sen ⁡ 25 ° ) - P g ( [ 7   m ] ⋅ cos ⁡ 55 ° - [ 16   m ⋅ cos ⁡ 55 ° ) = 0

Repara que para força peso tivemos que decompor para parte em duas partes de acordo com seu centro de gravidade.

Isso implica que:

T = ( 11000   N ) ( 16   m cos ⁡ 55 ° ) + 15000   N ( 7 m cos ⁡ 55 ° ) 13   m sen ⁡ 25 °

T = 2,93 × 10 4   N

Passo 3

b) E então, aplicando agora o equilíbrio das forças no eixo x , teremos que:

∑ F x = 0

Logo:

F h - T cos ⁡ 30 ° = 0

Isso implica que:

F h = 2,54 × 10 4   N

E aplicando agora no eixo y :

∑ F y = 0

Obtemos que:

F v - T sen ⁡ 30 ° - P g - P t = 0

E dessa forma:

F v = 4,06 × 10 4   N

Valeu, galera! Até a próxima! 😉

Resposta

  1. T = 2,93 × 10 4   N
  2. F h = 2,54 × 10 4   N e F v = 4,06 × 10 4   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando o pé de um corredor atinge o chão, a força de cisalhamento atuando sobre um solado de 8,0m m de espessura é como a mostrada na Figura 12-46. Se a força de 25N é distribuída sobre uma área de 15
Um cilindro, de massa M e raio R , rola até um degrau de altura h , como mostrado na figura. Quando uma força horizontal de magnitude F é aplicada no topo do cilindro, este permanece em repouso. (a) D
A Figura 12-62 mostra uma prancha homogênea, de 20 cm de comprimento, sobre um cilindro de 4,00 cm de raio. A massa da prancha é 5,0 kg e a do cilindro é 8,0 kg. O coeficiente de atrito estático entre
Um cubo maciço de aresta a, equilibrado sobre um cilindro de diâmetro d, está em equilíbrio instável se d ≪ a (Figura 12-64), e está em equilíbrio estável se d ≫ a . O cubo não escorrega sobre o cilin
Duas esferas maciças e polidas (sem atrito), de raio r, são colocadas dentro de um cilindro de raio R, como na Figura 12-63. A massa de cada esfera é m. Determine a força exercida pela base do cilindr