Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 14

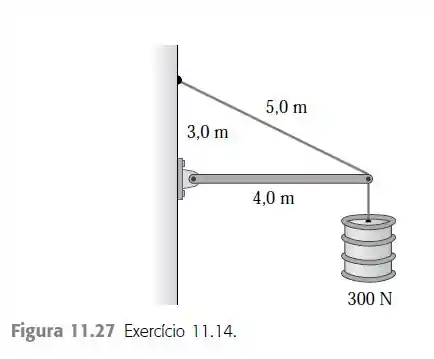
A viga horizontal da Figura 11.27 pesa 150   N e seu centro de gravidade está localizado em seu centro. Ache a) a tensão no cabo; b) as componentes horizontal e vertical da força exercida sobre a viga na parede.

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que uma viga horizontal pesa 150   N e seu centro de gravidade está localizado em seu centro.

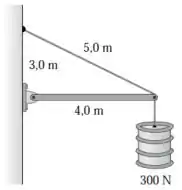
Queremos encontrar a tensão no cabo e as componentes horizontal e vertical da força exercida sobre a viga na parede.

Bom... Aqui a gente tem que perceber que o cabo sustenta tanto o barril como a viga. Então vamos aplicar a primeira e a segunda condições de equilíbrio na viga.

Dessas condições, queremos dizer que o somatório das forças F e dos torques τ são iguais a zero, ou seja:

∑ F = 0

∑ τ = 0

Passo 2

Mas primeiro, vamos esboçar um diagrama de corpo livre:

H v e H h são, respectivamente, as componentes vertical e horizontal da força exercida no feixe na parede (pela dobradiça).

Como o feixe é uniforme, seu centro de gravidade fica a 2,00 m de cada extremidade.

O ângulo θ pode ser calculado por trigonometria, já que o problema forneceu os lados do triangulo formado pela viga, parede e cabo.

Então temos:

cos ⁡ θ = 4 5 = 0,800

sen ⁡ θ = 3 5 = 0,600

A tensão T foi substituído por seus componentes x e y .

Passo 3

  1. Como o sistema está em equilíbrio, H v , H h e T x = T cos ⁡ θ   produzem um torque zero, ou seja,

    2. ∑ τ = 0

    Isso nos dá que:

    - P 2 m - P c a r g a 4 m + T sen ⁡ θ 4 m = 0

    E então,

    T = 150 N ⋅ 2 m + 300 N ⋅ 4 m 4 m ⋅ 0,600 = 625 N

    Passo 4

  2. Então, aplicando a segunda condição, temos que:

∑ F x = 0

H h = T cos ⁡ θ = 0

E isso implica que:

H h = 625 N ⋅ 0,800 = 500 N

E

∑ F y = 0

H v - P - P c a r g a + T sen ⁡ θ = 0

Isso implica que:

H v = P + P c a r g a + T sen ⁡ θ = 150 N + 300 N - 625 N 0,600 = 75 N

Resposta

  1. T = 625 N
  2. H h = 500 N e H v = 75 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas pessoas transportam uma prancha de madeira uniforme com 3,0 m de comprimento e peso de 160 N. Se uma das pessoas aplica em uma extremidade uma força de baixo para cimade 60 N, em qual ponto a out
Uma escada uniforme de 5,0m de comprimento repousa contra uma parede vertical sem atrito e sua extremidade inferior está situada a 3,0m da parede. A escada pesa 160N . O coeficiente de atrito estático
Determine a tensão T em cada cabo e o módulo, a direção e o sentido da força exercida sobre a viga pelo pivô em cada um dos arranjos indicados na Figura 11.26. Em cada caso, seja p o peso da caixa sus
Em um jardim zoológico, uma barra uniforme de 3,0 m de comprimento e 240 N é mantida em posição horizontal por meio de duas cordas amarradas em suas extremidades (Figura 11.30). A corda da esquerda fa
Uma porta de 1,0 m de largura e 2,0 m de altura pesa 280 N e é suportada por duas dobradiças, uma situada a 0,50 m a partir do topo e a outra a 0,50 m a partir do ponto inferior. Cada dobradiça suport