Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 99
Se prendermos dois blocos, de massas e , a cada uma das extremidades de um mola de constante de força , e o fizermos oscilar largando-os do repouso após distender a mola, mostre que a frequência de oscilação é dada por , onde é a massa reduzida do sistema.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. Ele quer a frequência de oscilação para um tipo diferentão de oscilação. Mas fica tranquilo, que tem um passo a passo para esse tipo de questão, tá? Fica firme e bora!
Vou te dar um bizu: quando ele pede isso, a primeira coisa é o diagrama de corpo livre da situação. Nosso diagrama vai ficar assim:
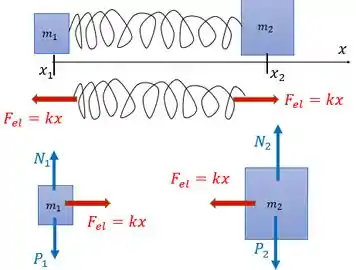
Repara que a força elástica sobre os blocos é a mesma e com sentidos opostos para que a mola permaneça em equilíbrio (somatório de forças sobre a mola seja zero), mas que os blocos estão em diferentes posições e .
Essa força é dada por
Vamos supor que a mola pode se encurtar muito, o bastante para que um bloco encoste no outro, assim essa distensão para cada bloco vai ser igual a diferença de posição entre eles
Passo 2
O próximo passo para esse tipo de questão é usar a segunda lei de Newton e escrever a aceleração que aparece nela como a segunda derivada da posição em relação ao tempo
Aplicando a segunda lei de Newton para o bloco da esquerda
Aplicando também no segundo bloco, temos:
Aparece esse sinal de menos ali porque a força sobre o segundo bloco aponta para o lado oposto de .
Passo 3
Agora queremos obter uma equação diferencial que rege esse movimento.
Temos duas equações diferenciais, porque estamos relacionando com sua derivada.
Vamos transforma-las em uma equação só fazendo uma menos a outra:
Mas lembra que , então:
Passo 4
Quase chegando lá. A massa reduzida tem essa fórmulinha:
Que pode até ser escrita como o enunciado diz se a gente rearrumar
Acontece que a primeira forma aparece na nossa equação, então vamos substituir:
Passo 5
Agora é o nosso último passo desse tipo de questão. A gente vai comparar essa equação diferencial que temos com a equação do oscilador harmônico.
Sabemos que a equação diferencial de um oscilador harmônico simples é dada por:
A solução desta equação é:
Onde:
Comparando as equações diferenciais
Vemos que a nossa vai ter uma solução similar porque as equações tem o mesmo formato, mas com . Então para o nosso oscilador, temos que
Onde:
E:
Resposta
Demonstração nos passos